There's a total of 9 articles.
Culling & Clipping → Read more...
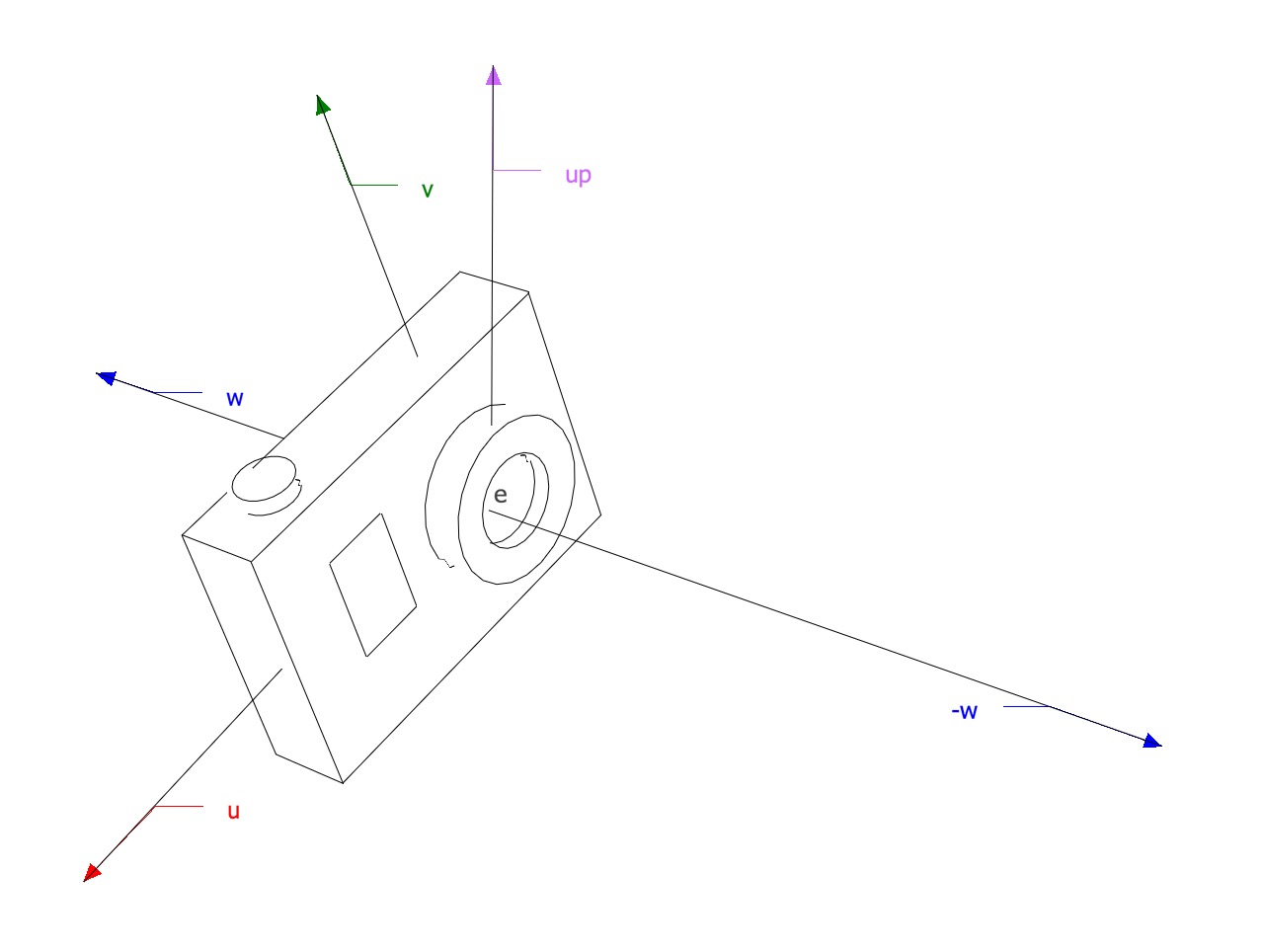
The math behind culling and clipping and how it’s related with the camera and with what it sees.
- Culling is a process where geometry that’s not visible from the camera is discarded to save processing time.
- Clipping is a process that removes parts of primitives that are outside the view volume (clipping against the six faces of the view volume).
Affine spaces → Read more...
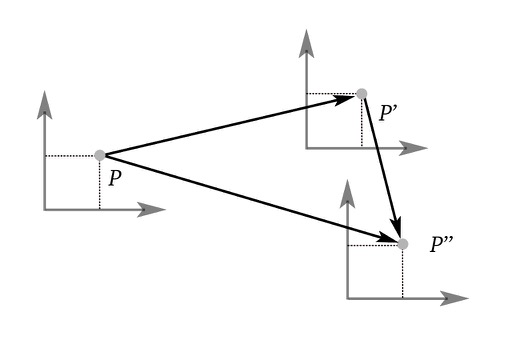
An affine space is a generalization of the notion of a vector space, but without the requirement of a fixed origin or a notion of “zero”.
Vector spaces → Read more...
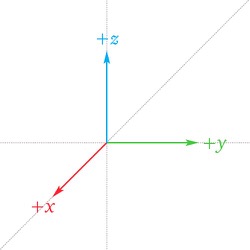
A vector space is a set whose elements are called “vectors” (denoted as $\v{v}$ or $\mathbf{v}$) which have two operations defined on them: addition of vectors and multiplication of an scalar by a vector.
This article covers some examples of vector spaces, basis of vectores spaces and linear maps.
Triangle in affine spaces → Read more...
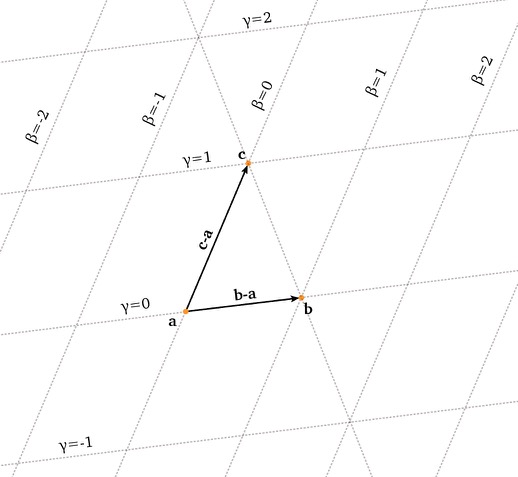
In an affine space any point can be represented by a sum of an origin point plus a set of scaled vector. This article covers defining all the points in a triangle in an affine space.
Geometric tests → Read more...
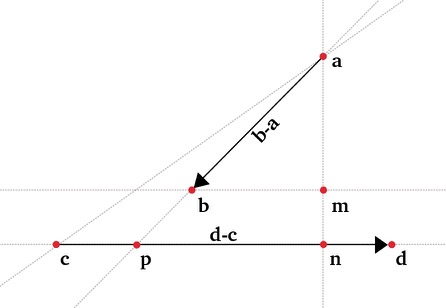
Different algorithms to test geometric properties like finding the intersection of two lines.
Normals → Read more...
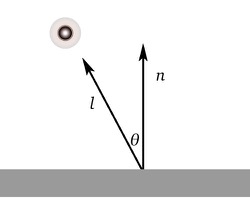
A normal vector to a curve at a particular point is a vector perpendicular to the tangent vector of the curve at that point (also called a gradient).
Projective space → Read more...
In projective geometry unlike euclidean geometry, two parallel lines meet at a point. Desargues introduced the concept of a line at finity where a point at infinity can be defined. This article covers the need of a point at infinity in projective space, the line at infinity and the projective plane.
Euler angles → Read more...
Euler angles are a way to describe the orientation of a rigid body with 3 values, these values represent 3 angles:
- yaw - Rotation around the vertical axis
- pitch - Rotation around the side-to-side axis
- roll - Rotation around the front-to-back axis
Transformation matrix → Read more...
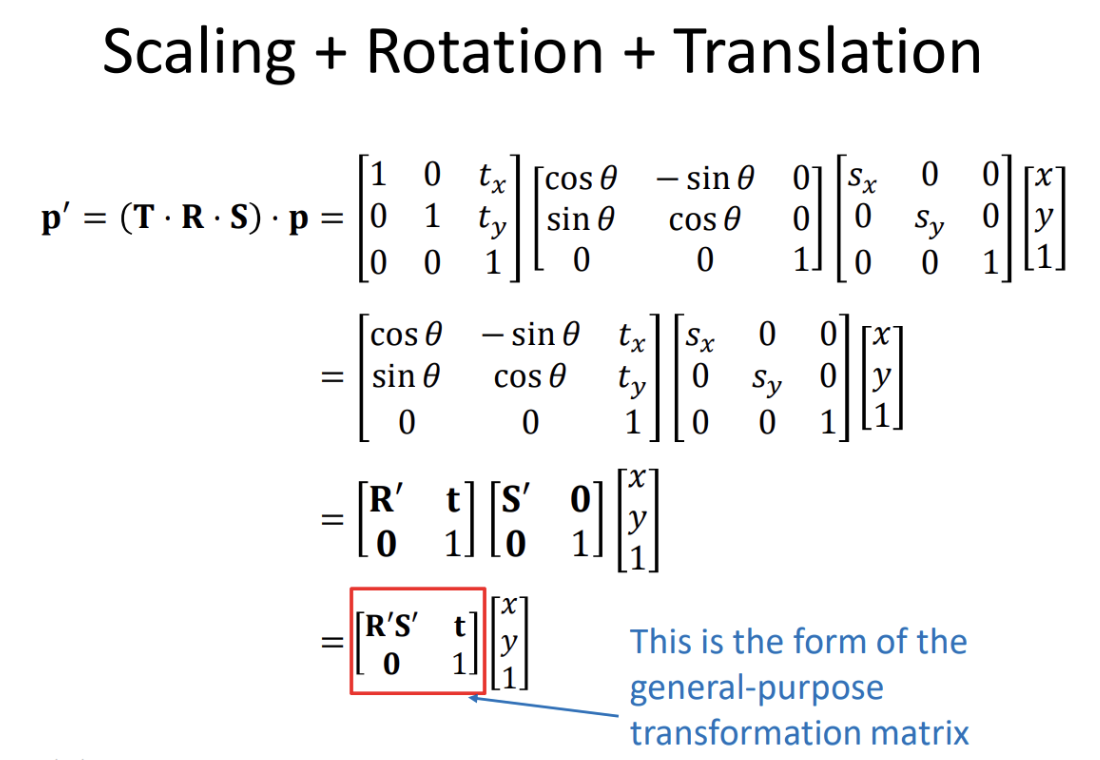
A linear transformation can be represented with a matrix which transforms vectors from one space to another. Transformation matrices allow arbitrary transformations to be displayed in the same format. Also matrices can be multiplied to enable composition. This article covers how to think and reason about these matrices and the way we can represent them (row vectors vs column vectors).