3d
There's a total of 10 articles.
Quaternions


Culling & Clipping
The math behind culling and clipping and how it’s related with the camera and with what it sees.
- Culling is a process where geometry that’s not visible from the camera is discarded to save processing time.
- Clipping is a process that removes parts of primitives that are outside the view volume (clipping against the six faces of the view volume).

Transformation matrix to transform objects from NDC coordinates to screen coordinates (viewport transform)
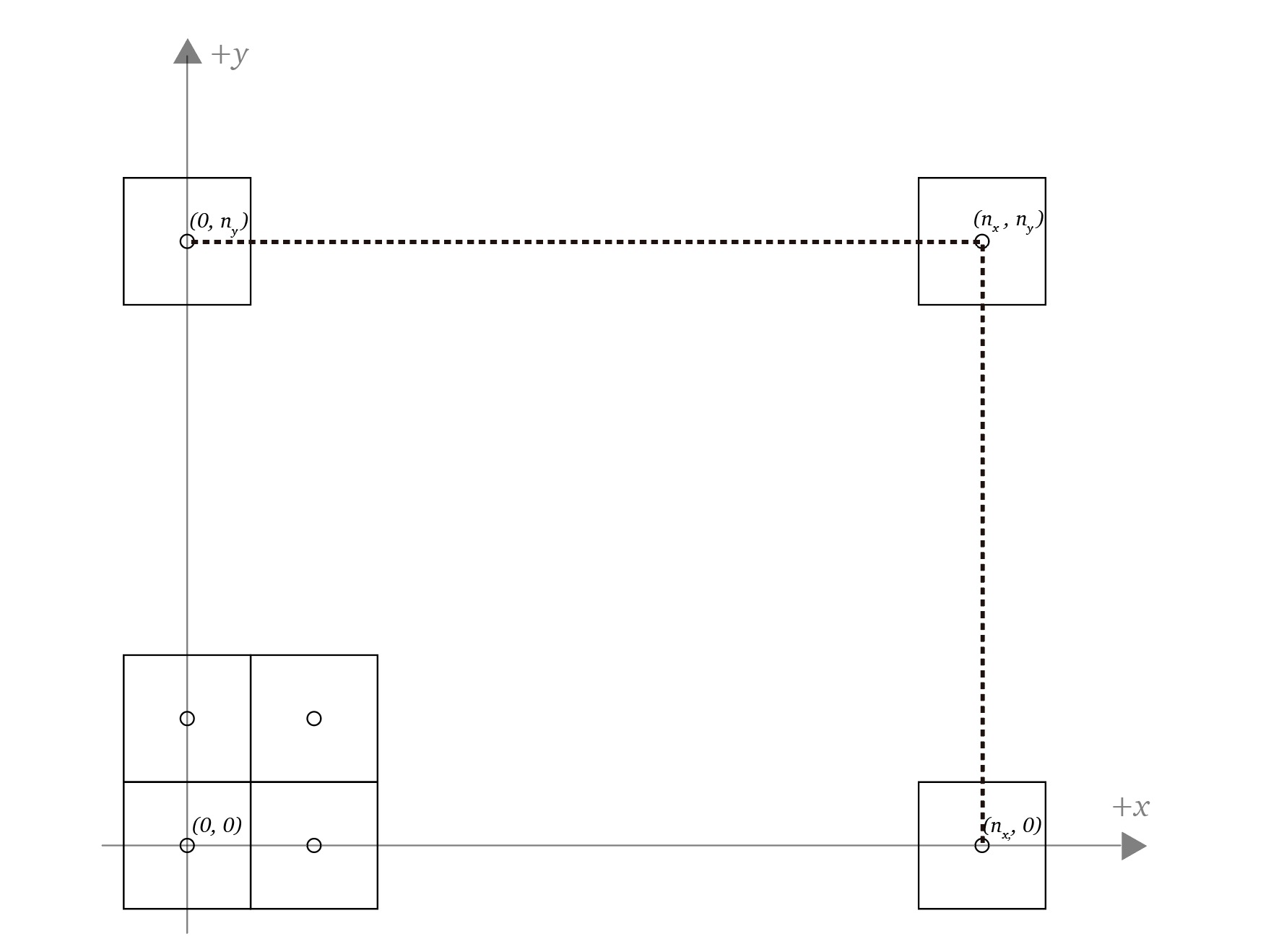
One matrix transformation in the 3D to a 2D transformation pipeline is the viewport transform where objects are transformed from normalized device coordinates (NDC) to screen coordinates (SC).
In short it's the transformation of numbers in the range [-1, 1] to numbers corresponding to pixels on the screen, which is a linear mapping computed with linear interpolation.
In this article I cover the math behind the generation of the viewport transformation matrix.

Transformation matrix for projection of 3D objects into a 2D plane (projection transform)
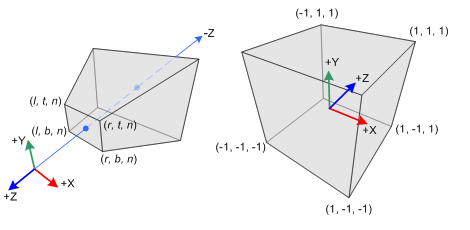
In Computer Graphics 3D objects created in an abstract 3D world will eventually need to be displayed in a screen, to view these objects in a 2D plane like a screen objects will need to be projected from the 3D space to the 2D plane with a transformation matrix.
In this article I cover two types of transformations: Orthographic projection and Perspective projection and analyze the math behind the transformation matrices.

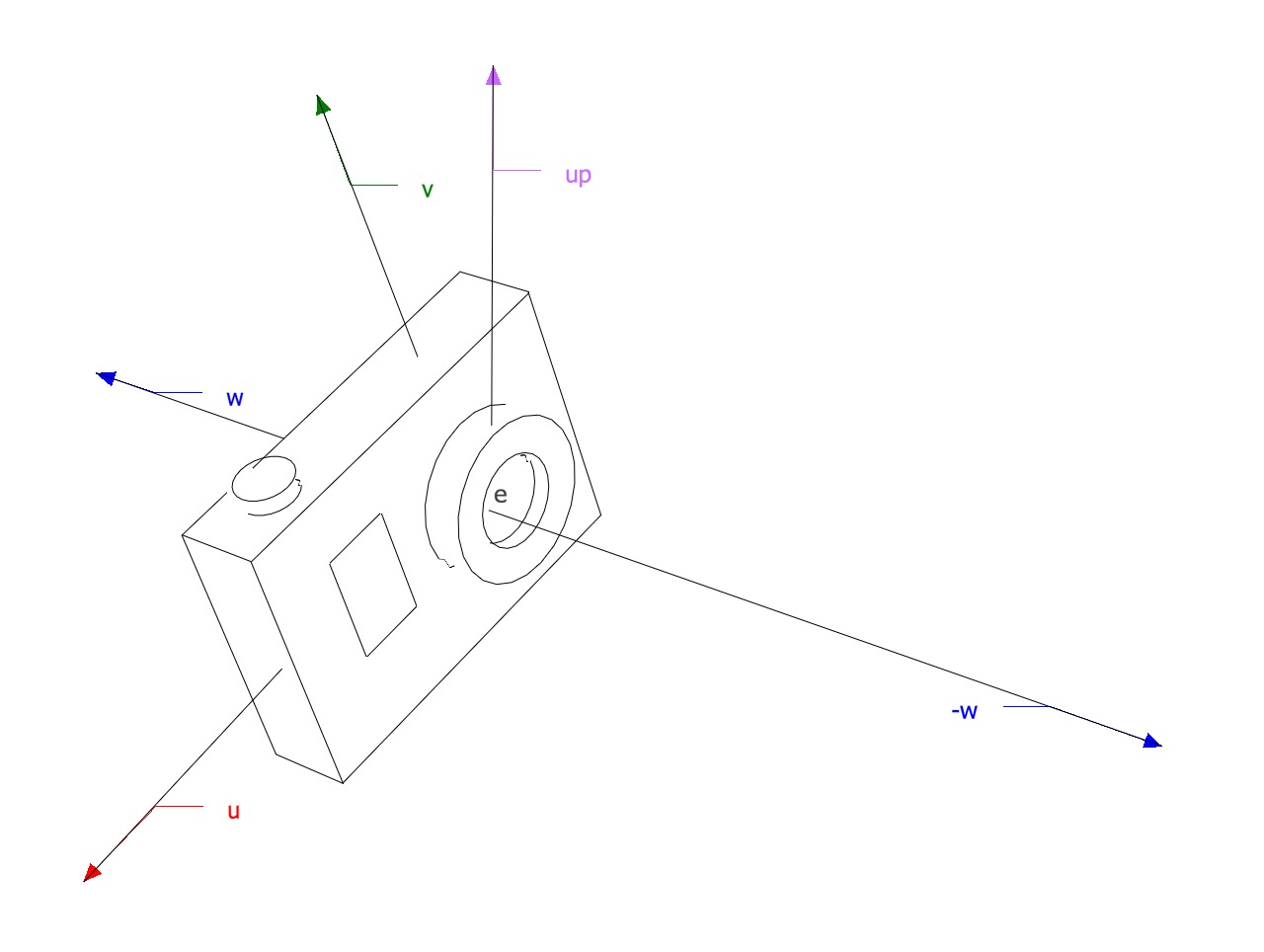
Transformation matrix to transform 3D objects from World Space to View Space (View transform)
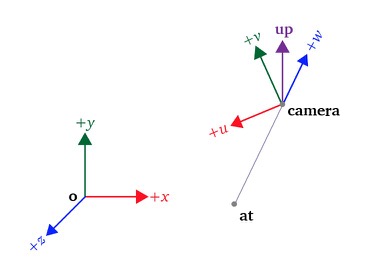
One matrix transformation in the 3D to a 2D transformation pipeline is the view transform where objects are transformed from world space to view space. a transformation matrix.
In this article I cover the math behind the generation of this transformation matrix.

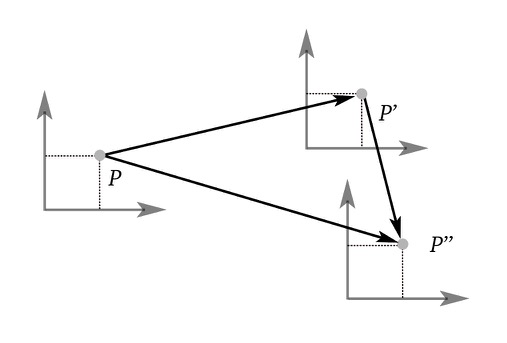
Translating objects with a Transformation Matrix

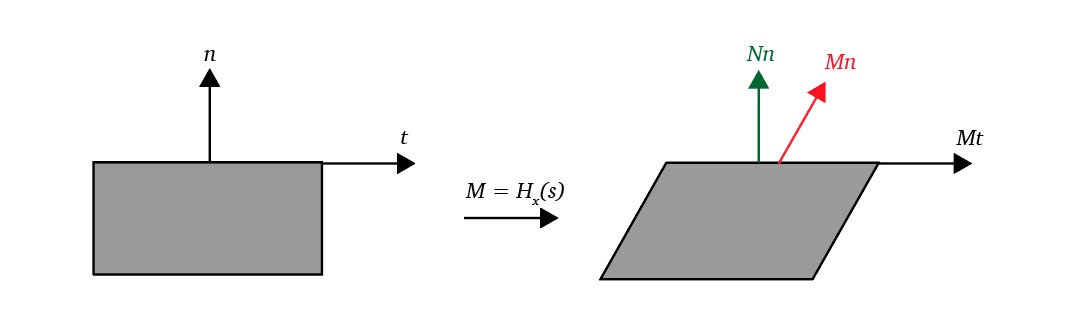
Shearing objects with a Transformation Matrix

Introduction to rotation for computer graphics

The basics of rotation in 2d and 3d for computer graphics with a focus on 3d rotation about cardinal axes and 3d rotation with quaternions.
For quaternions, please also look at https://eater.net/quaternions amazing animations!

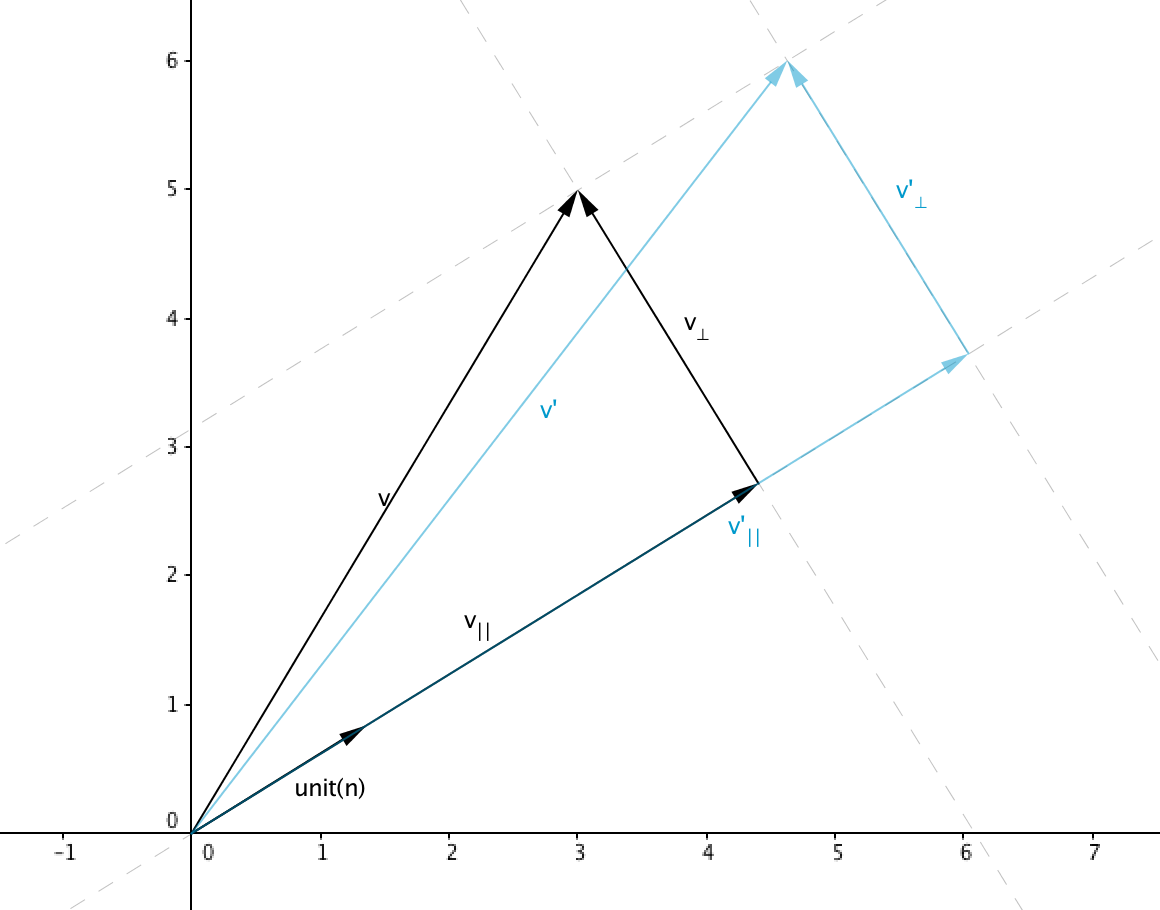
Scaling objects with a Transformation Matrix

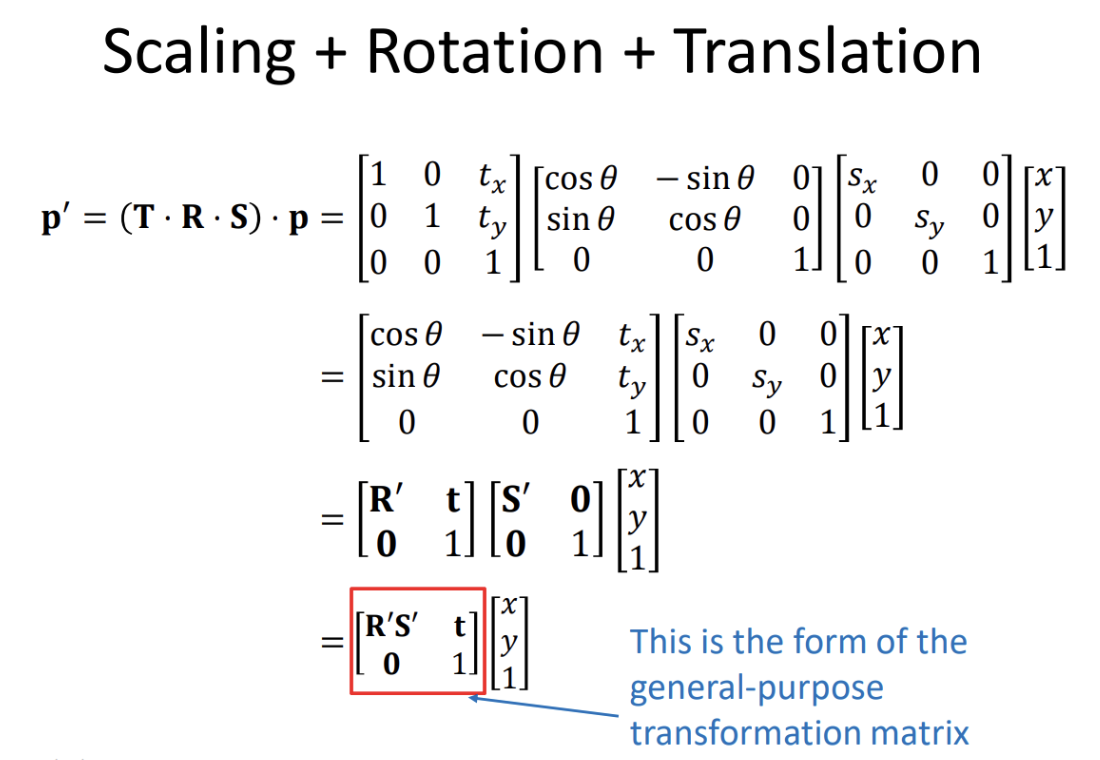
Transformation matrix