There's a total of 9 articles.
Transformation matrix to transform objects from NDC coordinates to screen coordinates (viewport transform) → Read more...
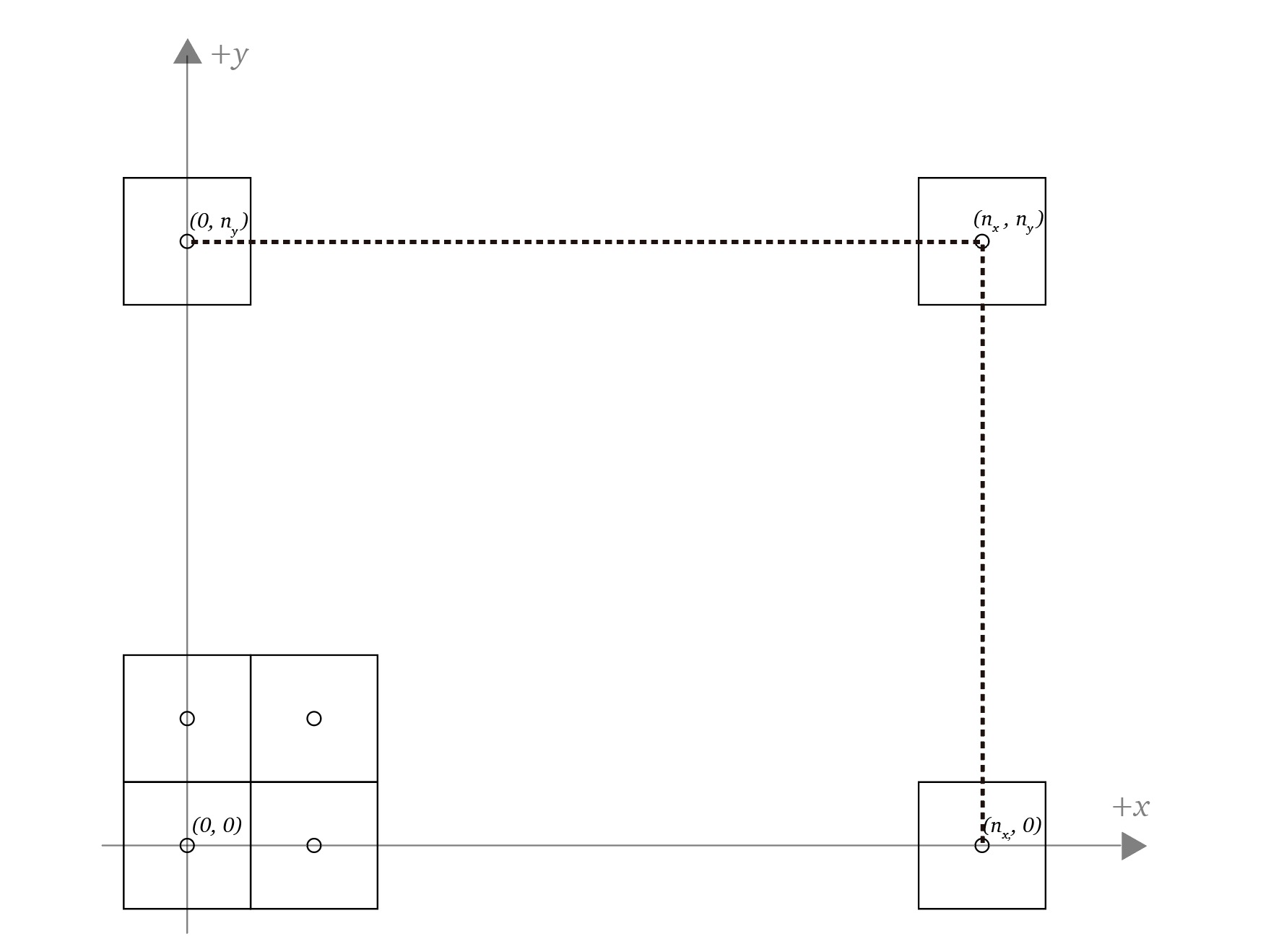
One matrix transformation in the 3D to a 2D transformation pipeline is the viewport transform where objects are transformed from normalized device coordinates (NDC) to screen coordinates (SC).
In short it’s the transformation of numbers in the range [-1, 1] to numbers corresponding to pixels on the screen, which is a linear mapping computed with linear interpolation.
In this article I cover the math behind the generation of the viewport transformation matrix.
Transformation matrix for projection of 3D objects into a 2D plane (projection transform) → Read more...
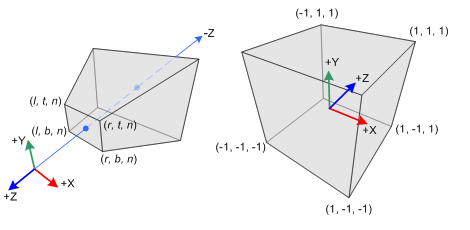
In Computer Graphics 3D objects created in an abstract 3D world will eventually need to be displayed in a screen, to view these objects in a 2D plane like a screen objects will need to be projected from the 3D space to the 2D plane with a transformation matrix.
In this article I cover two types of transformations: Orthographic projection and Perspective projection and analyze the math behind the transformation matrices.
Transformation matrix to transform 3D objects from World Space to View Space (View transform) → Read more...
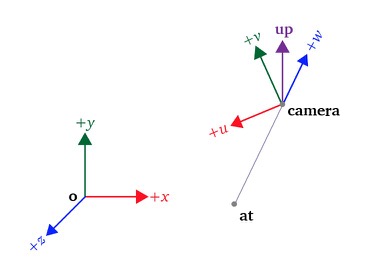
One matrix transformation in the 3D to a 2D transformation pipeline is the view transform where objects are transformed from world space to view space. a transformation matrix.
In this article I cover the math behind the generation of this transformation matrix.
Combining Matrix Transformations → Read more...
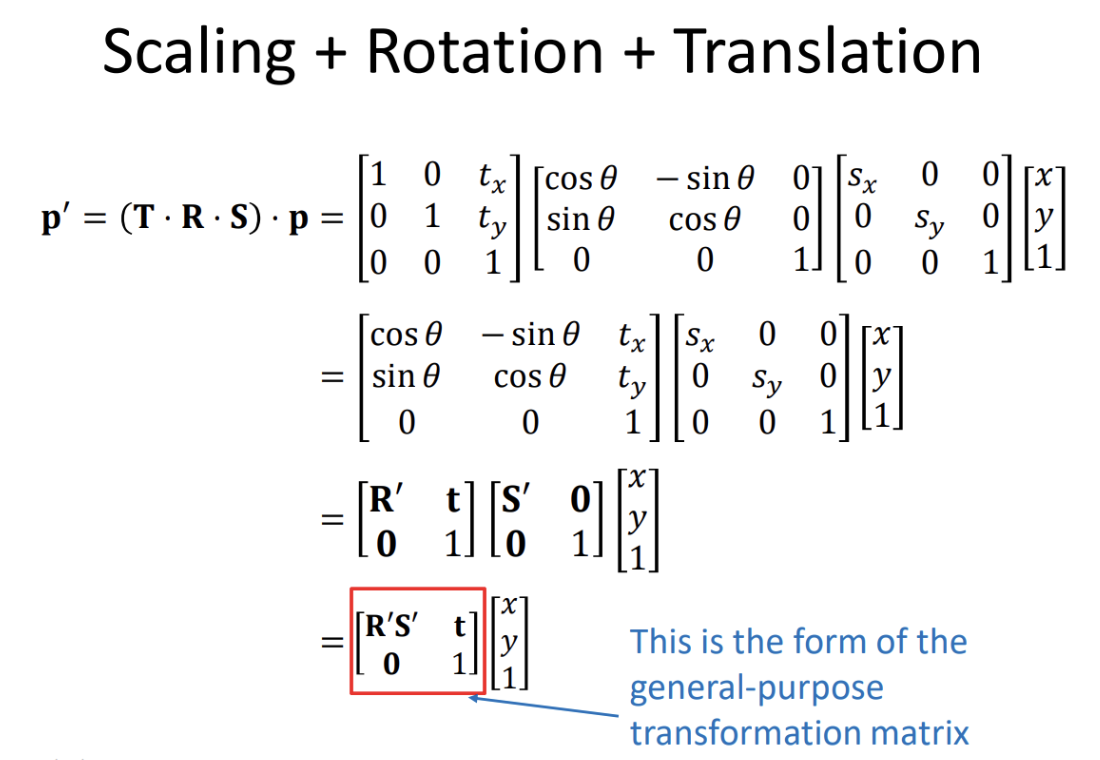
Taking multiple matrices each encoding a single transformations and combining them is how we transform vectors between different spaces. This article creating a transformation matrix that combines a rotation followed by a translation, a translation followed by a rotation and creating transformation matrices to transform between different coordinate systems.
Translating objects with a Transformation Matrix → Read more...
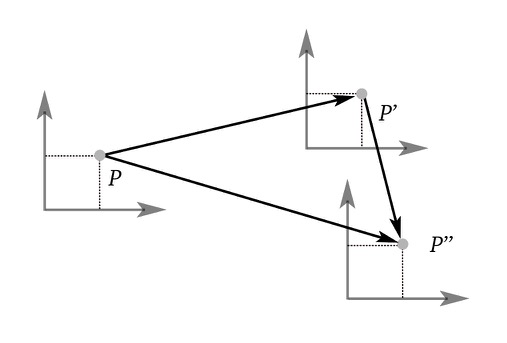
We build different types of transformation matrices to translate objects along cardinal axes, arbitrary axes in 2d and 3d with matrix multiplication!
Shearing objects with a Transformation Matrix → Read more...
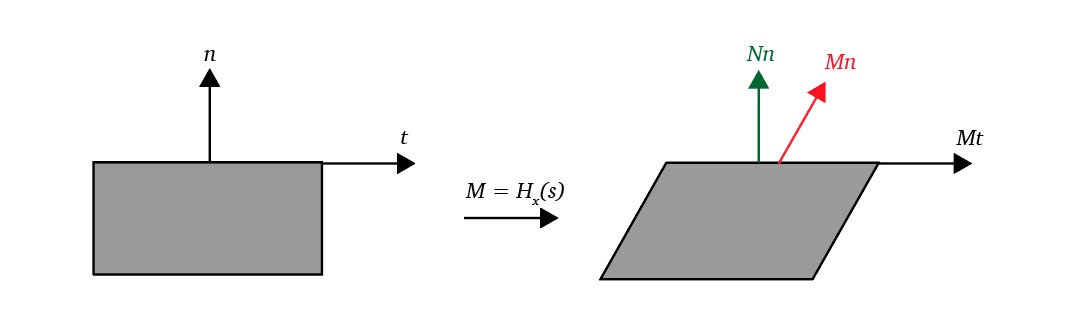
Shearing is a transformation that skews the coordinate space, the idea is to add a multiple of one coordinate to the other
Scaling objects with a Transformation Matrix → Read more...
We build different types of transformation matrices to scale objects along cardinal axes, arbitrary axes in 2d and 3d with matrix multiplication!
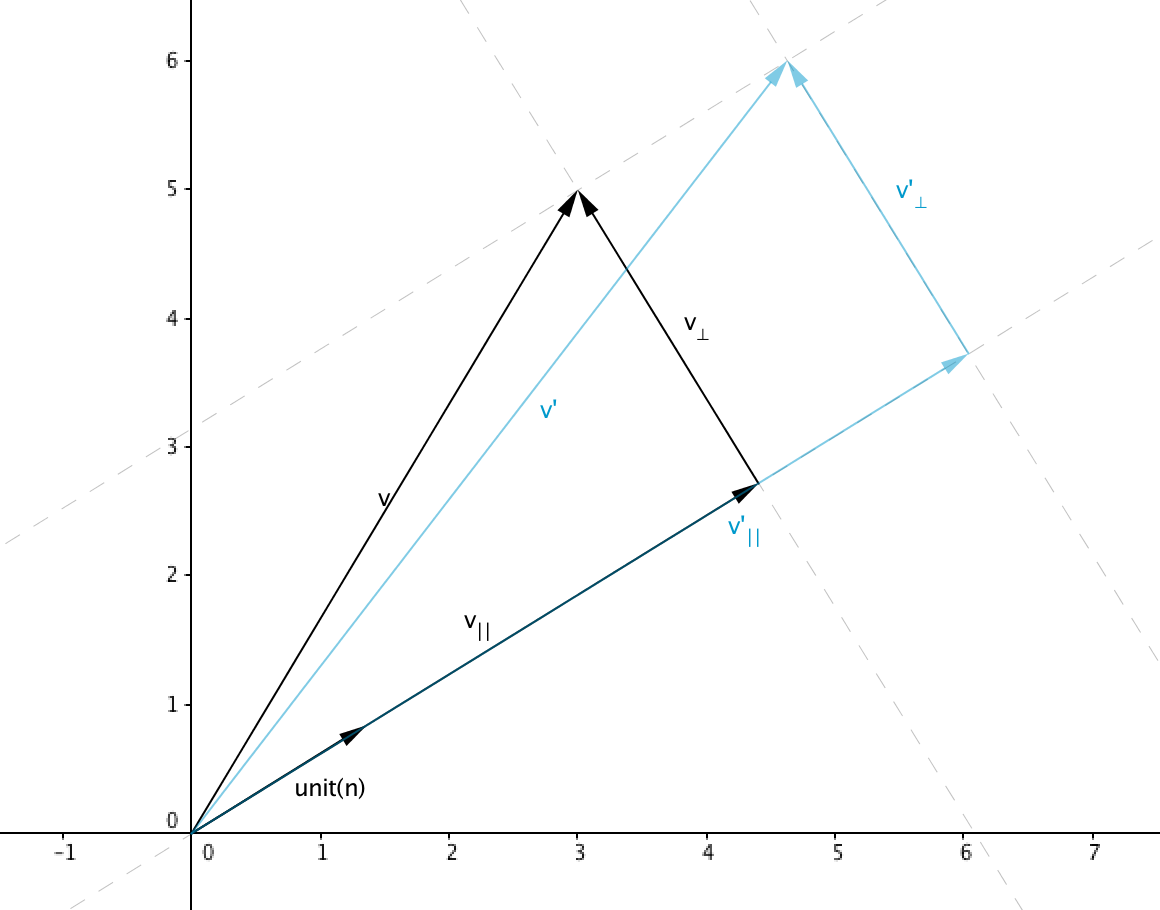
Transformation matrix → Read more...
A linear transformation can be represented with a matrix which transforms vectors from one space to another. Transformation matrices allow arbitrary transformations to be displayed in the same format. Also matrices can be multiplied to enable composition. This article covers how to think and reason about these matrices and the way we can represent them (row vectors vs column vectors).
Coordinate systems and transformations between them → Read more...
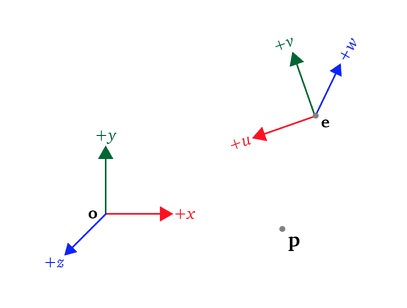
The position and orientation of an object in real life can be described with direction and magnitude e.g. the TV is 3 meters in front of me. While that description is good for me it might be that for someone else in a room the TV is 5 meters to the right of that person. Information about objects are given in the context of a reference frame. Usually in Computer Graphics objects need to be expressed with respect to the camera frame, this article covers why we need to have multiple reference frames as well as the math needed to express objects in a different reference frame.