There's a total of 7 articles.
Building a first person shooter camera in C++ → Read more...
A first person camera captures objects from the viewpoint of a player’s character. Some aspects have to be considered like the characteristics of the camera (orbiting with the mouse and translation with keyboard keys) as well as how we could capture all these characteristics with math and linear algebra.
In this article I analyze the math needed to design and implement a 1st person shooter camera in C++.
Eigenvalues and eigenvectors → Read more...
An eigenvalue represents how the object scales (or stretches/compresses) a particular direction (or eigenvector) when acted upon by the object. This article covers how to find these values in a square matrix as well as how it’s applicable in compute graphics.
Combining Matrix Transformations → Read more...
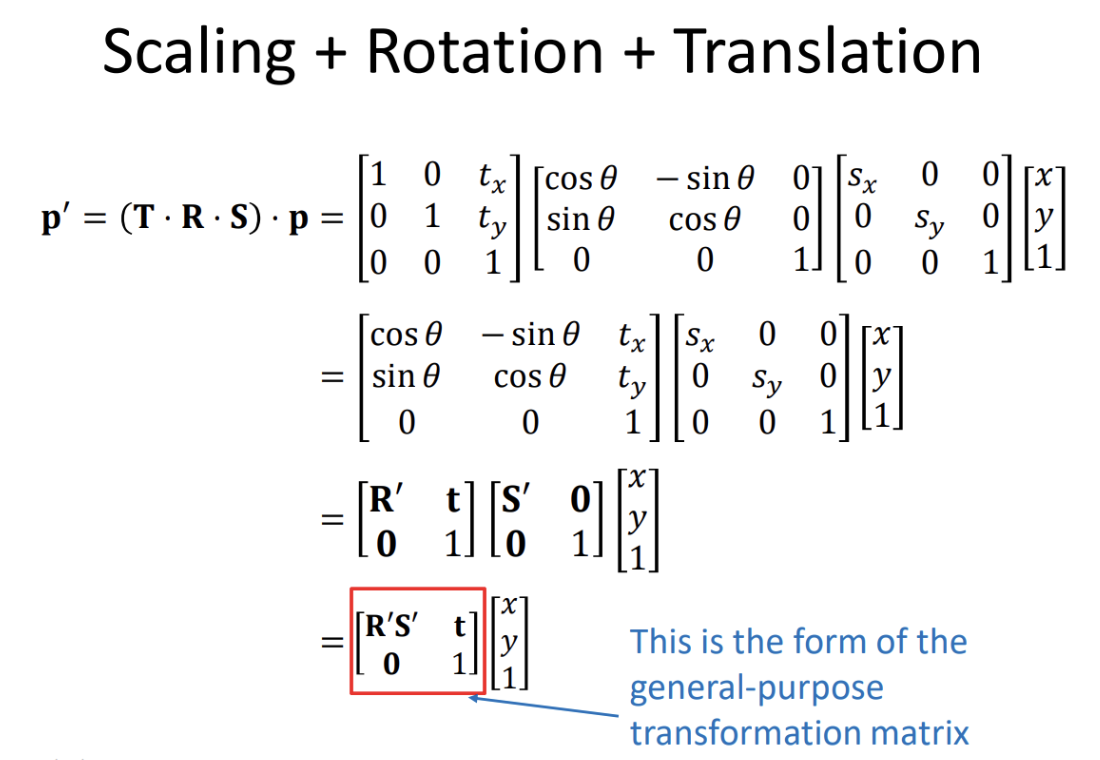
Taking multiple matrices each encoding a single transformations and combining them is how we transform vectors between different spaces. This article creating a transformation matrix that combines a rotation followed by a translation, a translation followed by a rotation and creating transformation matrices to transform between different coordinate systems.
Translating objects with a Transformation Matrix → Read more...
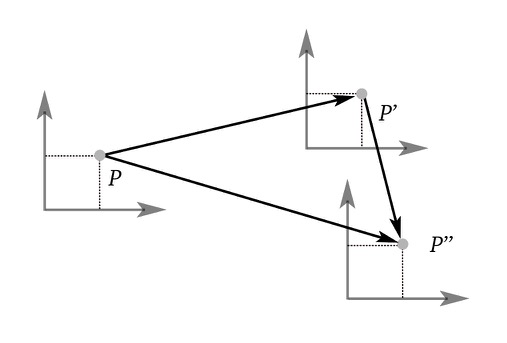
We build different types of transformation matrices to translate objects along cardinal axes, arbitrary axes in 2d and 3d with matrix multiplication!
Shearing objects with a Transformation Matrix → Read more...
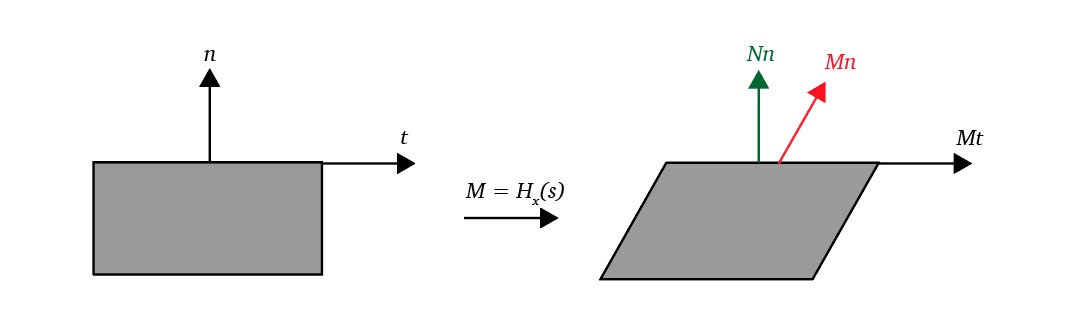
Shearing is a transformation that skews the coordinate space, the idea is to add a multiple of one coordinate to the other
Scaling objects with a Transformation Matrix → Read more...
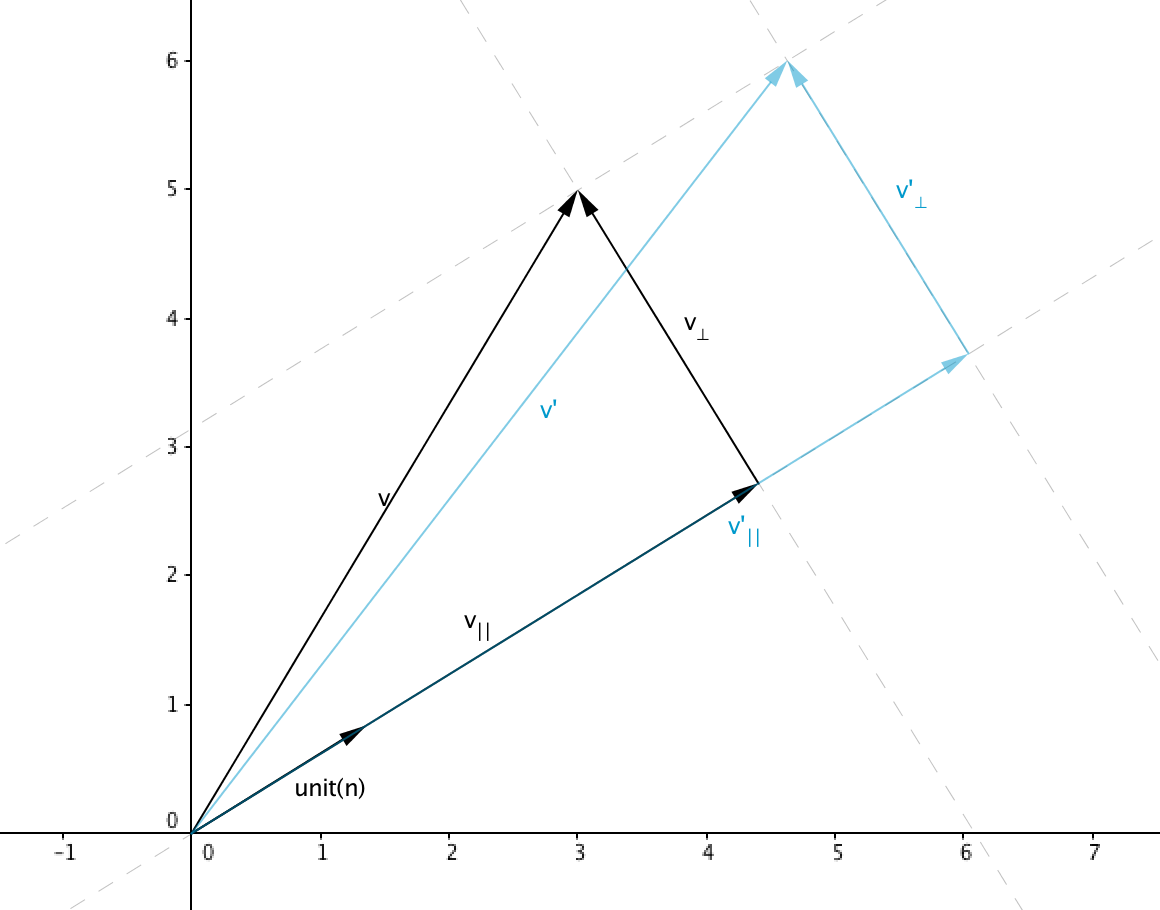
We build different types of transformation matrices to scale objects along cardinal axes, arbitrary axes in 2d and 3d with matrix multiplication!
Transformation matrix → Read more...
A linear transformation can be represented with a matrix which transforms vectors from one space to another. Transformation matrices allow arbitrary transformations to be displayed in the same format. Also matrices can be multiplied to enable composition. This article covers how to think and reason about these matrices and the way we can represent them (row vectors vs column vectors).