Transformation matrix

Let’s say that we’re given the standard basis vectors $i = [1, 0, 0],; j = [0, 1, 0],; k = [0, 0, 1]$ and we multiply each of these vectors by an arbitrary matrix $M$

\begin{aligned} iM & = [\begin{array}{c} 1 & 0 & 0 \end{array}] [\begin{array}{c} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array}] = [\begin{array}{c} m_{11} & m_{12} & m_{13} \end{array}] \\ jM & = [\begin{array}{c} 0 & 1 & 0 \end{array}] [\begin{array}{c} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array}] = [\begin{array}{c} m_{21} & m_{22} & m_{23} \end{array}] \\ kM & = [\begin{array}{c} 0 & 0 & 1 \end{array}] [\begin{array}{c} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array}] = [\begin{array}{c} m_{31} & m_{32} & m_{33} \end{array}] \end{aligned}

The first row of $M$ contains the result of performing a transformation on the vector $i$ , the second row is the result of transforming $j$ and third row to $k$

Let $v$ be some vector expressed under this coordinate space which means that it can be represented as a linear combination of the basis

v = v_{x} i + v_{y} j + v_{z} k

If we multiply this vector by the matrix $M$

\begin{aligned} v^{'} = vM & = (v_{x} i + v_{y} j + v_{z} k) M \\ = v_{x} (iM) + v_{y} (jM) + v_{z} (kM) \\ (1) & = v_{x} [\begin{array}{c} m_{11} & m_{12} & m_{13} \end{array}] + v_{y} [\begin{array}{c} m_{21} & m_{22} & m_{23} \end{array}] + v_{z} [\begin{array}{c} m_{31} & m_{32} & m_{33} \end{array}] \end{aligned}

If we let $M$ have the form

M = [\begin{matrix} - p - \\ - q - \\ - r - \end{matrix}]

Then $(1)$ can be rewritten as

v^{'} = vM = v_{x} p + v_{y} q + v_{z} r

$vM$ is a linear combination of the rows of $M$ , if we interpret these row vectors as the basis vectors of some coordinate system expressed/measured in terms of an outer coordinate system then we have successfully created a structure that encodes a space coordinate transformation (from object space to upright space) in the form of a matrix

v^{'} = vM = [\begin{matrix} v_{x} & v_{y} & v_{z} \end{matrix}] [\begin{matrix} - p - \\ - q - \\ - r - \end{matrix}] = v_{x} p + v_{y} q + v_{z} r

Another way to see this is that $M$ encodes in its rows a transformation made to the standard basis vectors $i, j, k$

The following notation means the rotation matrix that transforms the frame $a$ to the frame $b$ and that is represented in the frame $c$

^{c} M_{a \to b}

If the frame $c$ is equal to the frame $b$ then it can be omitted since it’s assumed that the matrix is represented in terms of the frame $b$

M_{a \to b}

For example the matrix that transform from object space to upright space is represented as

M_{o b j e c t \to u p r i g h t}

Transforming the vector $v_{object}$ expressed in object space to upright space is then

v_{u p r i g h t} = v_{o b j e c t} M_{o b j e c t \to u p r i g h t}

Row versus column vectors

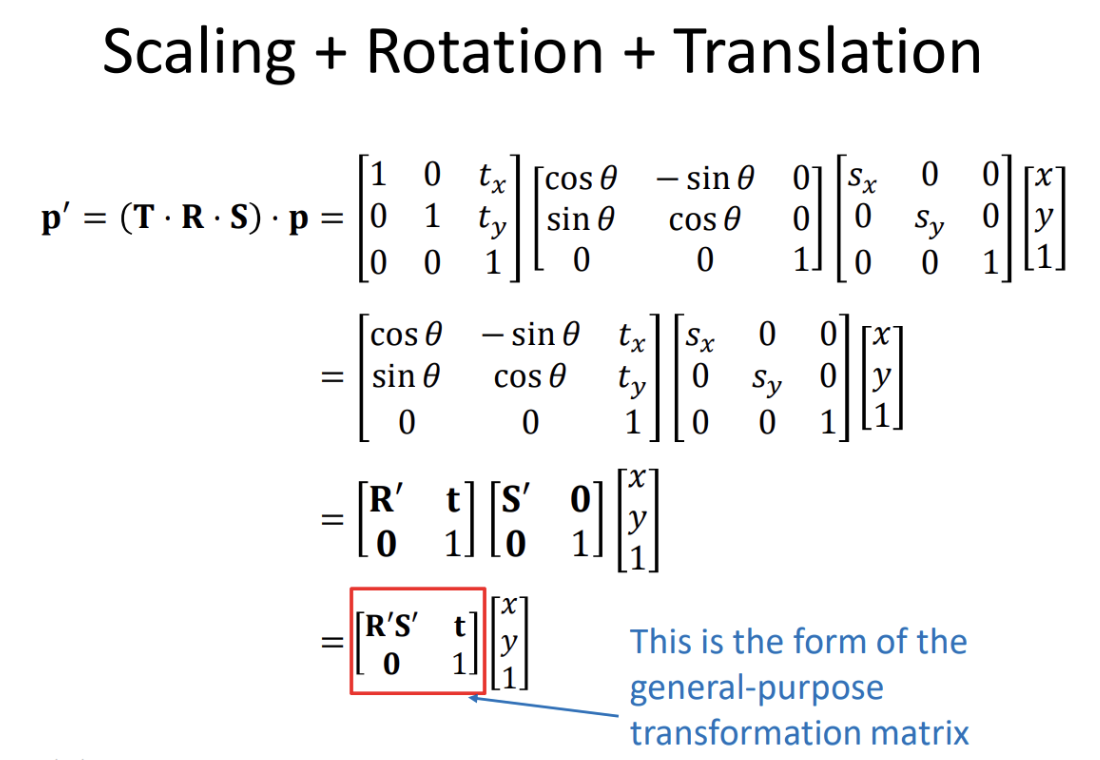
A space coordinate transform operation has the form

v^{'} = vM

Where $M$ encodes in its rows a transformation made to the standard basis vectors and $v^{'}$ and $v$ are row vectors

Let’s say that we want to transform a row vector by the matrices $A$ , $B$ and $C$ in that order, the operation is represented as

v^{'} = vABC

However it could be possible that $v$ is instead a column vector, in that case also $v^{'}$ must be a column vector, for $v^{'}$ to have the correct result we must pre-multiply $v$ by the transpose of the transformation matrix which is equivalent to transposing both sides of the equation

\begin{aligned} v^{'} & = vABC \\ {v^{'}}^{T} & = (vABC)^{T} & transposing both sides \\ {v^{'}}^{T} & = C^{T} B^{T} A^{T} v^{T} & because of the matrix transpose properties \end{aligned}

Note that

the transformations matrices $A^{T}$ , $B^{T}$ and $C^{T}$ encode in their columns a transformation made to the standard basis vectors i.e. they have the form

M = [\begin{matrix} p_{3 \times 1} & q_{3 \times 1} & r_{3 \times 1} \end{matrix}] where p = [\begin{matrix} p_{x} \\ p_{y} \\ p_{z} \end{matrix}], q = [\begin{matrix} q_{x} \\ q_{y} \\ q_{z} \end{matrix}] and r = [\begin{matrix} r_{x} \\ r_{y} \\ r_{z} \end{matrix}]

In Dunn & Parberry’s book a column vector inside a matrix is written as

M = [\begin{matrix} \overset{|}{\underset{|}{p}} & \overset{|}{\underset{|}{q}} & \overset{|}{\underset{|}{r}} \end{matrix}]

Also note that in this notation the arrow that connects the frames involved in the transformation is reversed, for example the transformation matrix that transform from object space to upright space is

M_{u p r i g h t \leftarrow o b j e c t}

In computer graphics column vectors should be used to represent points, differences between points and the likes