Shearing objects with a Transformation Matrix

This article is part 3 in the series about transformation matrices:

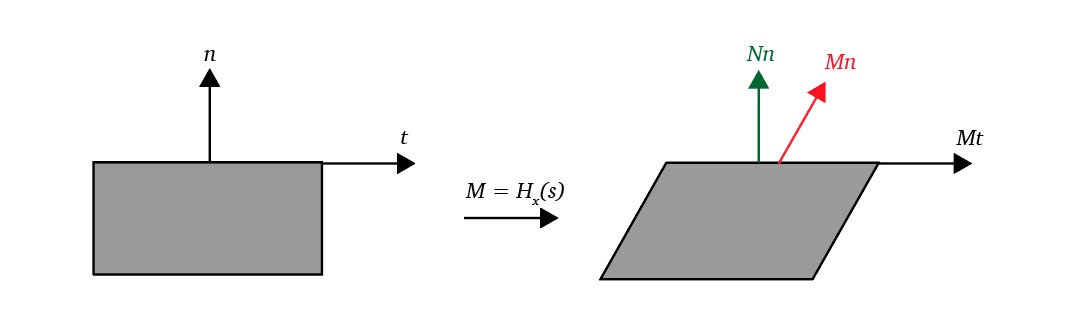
2D shearing

In 2D we can skew points towards the $x$ axis by making $x^{'} = x + s y$ , if $s > 0$ then points will skew towards the positive $x$ -axis, if $s < 0$ points will move towards the negative $x$ -axis

The transformation matrix that skews points towards the $x$ axis is

\begin{matrix} (1) & H_{x} (s) = [\begin{matrix} 1 & s \\ 0 & 1 \end{matrix}] \end{matrix}

Towards the $y$ axis is

\begin{matrix} (2) & H_{y} (s) = [\begin{matrix} 1 & 0 \\ s & 1 \end{matrix}] \end{matrix}

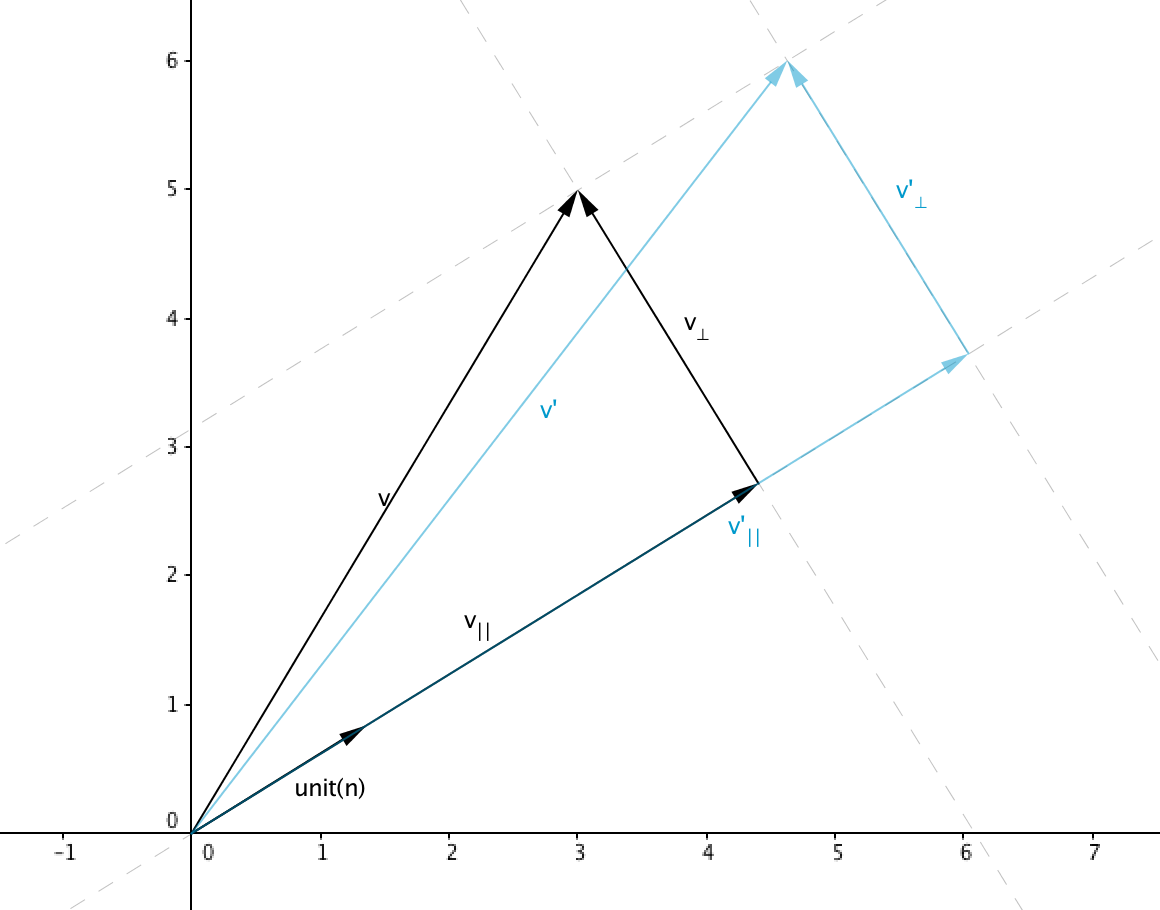
For example a vector $v$ multiplied by $(1)$ results in

v^{'} = H_{x} (s) v = [\begin{matrix} 1 & s \\ 0 & 1 \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \end{matrix}] = [\begin{matrix} v_{x} + s v_{y} \\ v_{y} \end{matrix}]

3D shearing

The notation $H_{xy}$ indicates that the $x$ and $y$ coordinates are shifted by the other coordinate $z$ i.e.

\begin{aligned} x^{'} & = x + s z \\ y^{'} & = y + t z \\ z^{'} & = z \end{aligned}

The shearing matrices in 3D are

\begin{matrix} (3) & H_{xy} (s, t) = [\begin{matrix} 1 & 0 & s \\ 0 & 1 & t \\ 0 & 0 & 1 \end{matrix}] \end{matrix}

\begin{matrix} (4) & H_{xz} (s, t) = [\begin{matrix} 1 & s & 0 \\ 0 & 1 & 0 \\ 0 & t & 1 \end{matrix}] \end{matrix}

\begin{matrix} (5) & H_{yz} (s, t) = [\begin{matrix} 1 & 0 & 0 \\ s & 1 & 0 \\ t & 0 & 1 \end{matrix}] \end{matrix}

For example a vector $v$ multiplied by $(3)$ results in

v^{'} = H_{xy} (s, t) v = [\begin{matrix} 1 & 0 & s \\ 0 & 1 & t \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix}] = [\begin{matrix} v_{x} + s v_{z} \\ v_{y} + t v_{z} \\ v_{z} \end{matrix}]