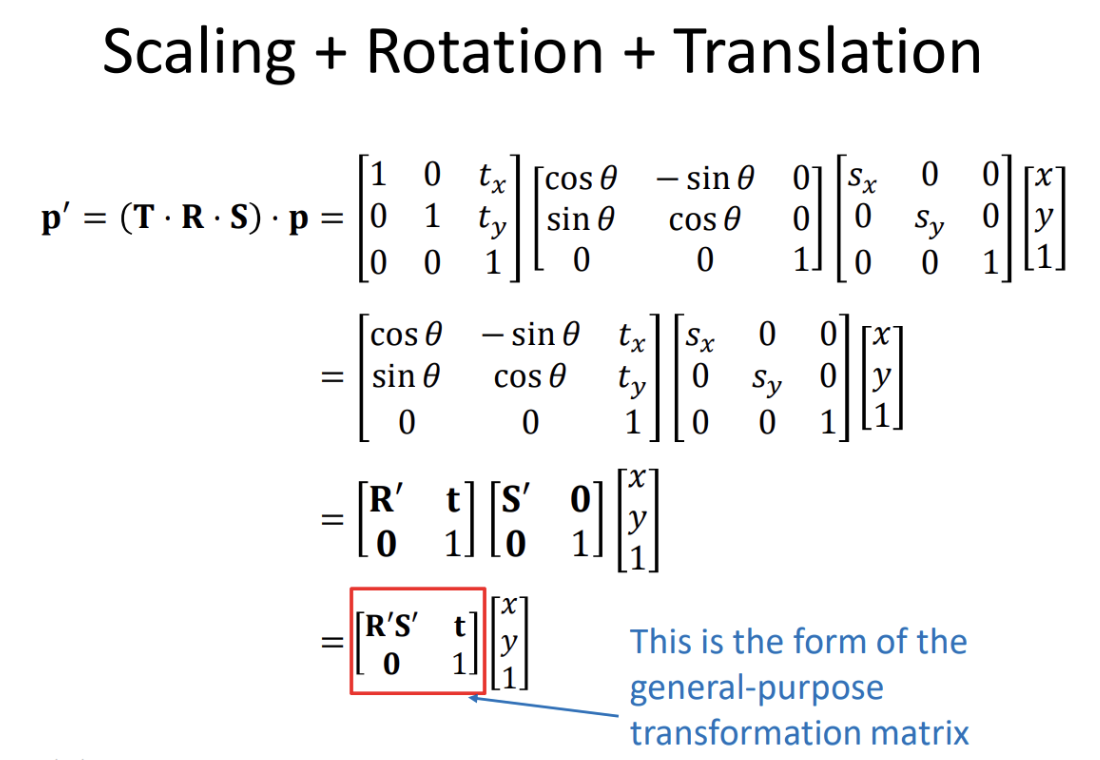
Given a square matrix $\mathbf{M}$:

• An eigenvector $\mathbf{v}$ is a non-zero vector whose direction doesn’t change when multiplied by $\mathbf{M}$. Note that if $\mathbf{M}$ has an eigenvector, then there are an infinite number of eigenvectors (vectors parallel to $\mathbf{v}$).
• An eigenvalue $\lambda$ is the scale factor associated with an eigenvector $\mathbf{v}$ of $\mathbf{M}$ after multiplication by $\mathbf{M}$.

Assuming that $\mathbf{M}$ has at least one eigenvector $\mathbf{v}$, we can perform standard matrix multiplications to find it. First, let’s manipulate the right side of $\text{(1)}$ so that it also features a matrix multiplication.

Where $\mathbf{I}$ is the identity matrix, next we can rewrite the last equation as

Because matrix multiplication is distributive

The quantity $\mathbf{M}-\lambda \mathbf{I}$ must not be invertible. If it had an inverse, we could premultiply both sides by $(\mathbf{M}-\lambda \mathbf{I}{)}^{-1}$, which would yield

The vector $\mathbf{v}\mathbf{=}\mathbf{0}$ fulfills $\text{(1)}$. However, we’ll try to find a vector $\mathbf{v}\ne \mathbf{0}$. If such a condition is added, then the matrix $\mathbf{M}-\lambda \mathbf{I}$ must not have an inverse, which also means that its determinant is 0.

If $\mathbf{M}$ is a $2\times 2$ matrix, then

From $\text{(???)}$, we can find two values for $\lambda$, which may be unique or imaginary. A similar manipulation for an $n\times n$ matrix will yield an $n$th degree polynomial. For $n\le 4$, we can compute the solutions by analytical methods; for $n>4$, only numeric methods are used.

The associated eigenvector can be found by solving $\text{(2)}$

Applications

List of applications

• If $\mathbf{M}$ is a transformation matrix, then $\mathbf{v}$ is a vector that isn’t affected by the rotation part of $\mathbf{M}$. Therefore, $\mathbf{v}$ is the rotation axis of $\mathbf{M}$.