This article is part 2 in the series about transformation matrices:

Scaling along the cardinal axes

Intuitively the basis vectors should be multiplied by an scalar, also they are independently affected by the scale factors

In 2D the basis vectors become

$$ \mathbf{p'} = k_x \mathbf{p} = k_x \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} k_x \\ 0 \end{bmatrix} \\ \mathbf{q'} = k_y \mathbf{q} = k_y \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ k_y \end{bmatrix} $$

Constructing the 2D scale matrix $\mathbf{S}(k_x, k_y)$ from these basis vectors

$$ \mathbf{S}(k_x, k_y) = \begin{bmatrix} k_x & 0 \\ 0 & k_y \end{bmatrix} $$

Similarly the 3D scale matrix is given by

$$ \mathbf{S}(k_x, k_y, k_z) = \begin{bmatrix} k_x & 0 & 0 \\ 0 & k_y & 0 \\ 0 & 0 & k_z \end{bmatrix} $$

Scaling along an arbitrary axis

Let $\unit{n}$ be the unit vector parallel to the direction of scale and $k$ to be the scale factor, a vector transformed by this scale operations can be represented as

$$ \mathbf{v'} = \mathbf{S}(\unit{n}, k) \mathbf{v} $$
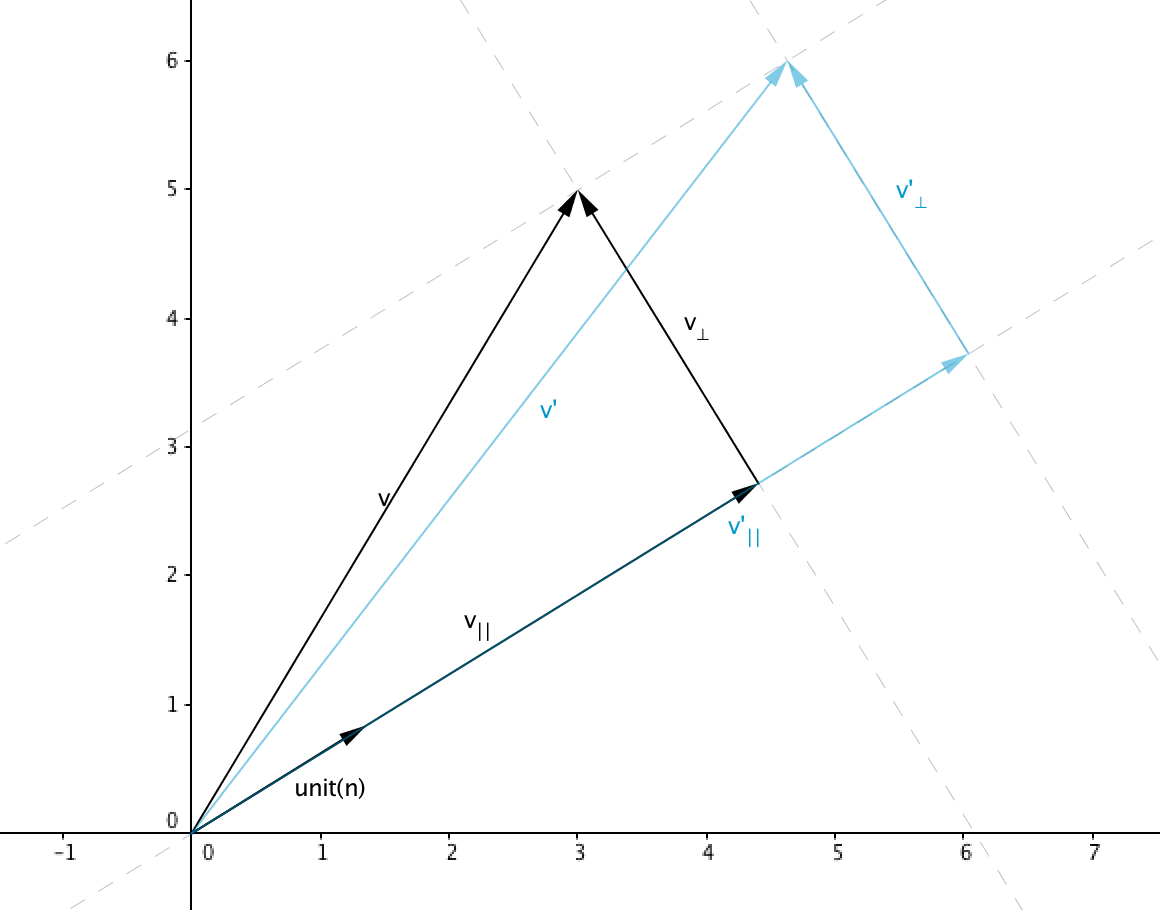
scale arbitrary axis

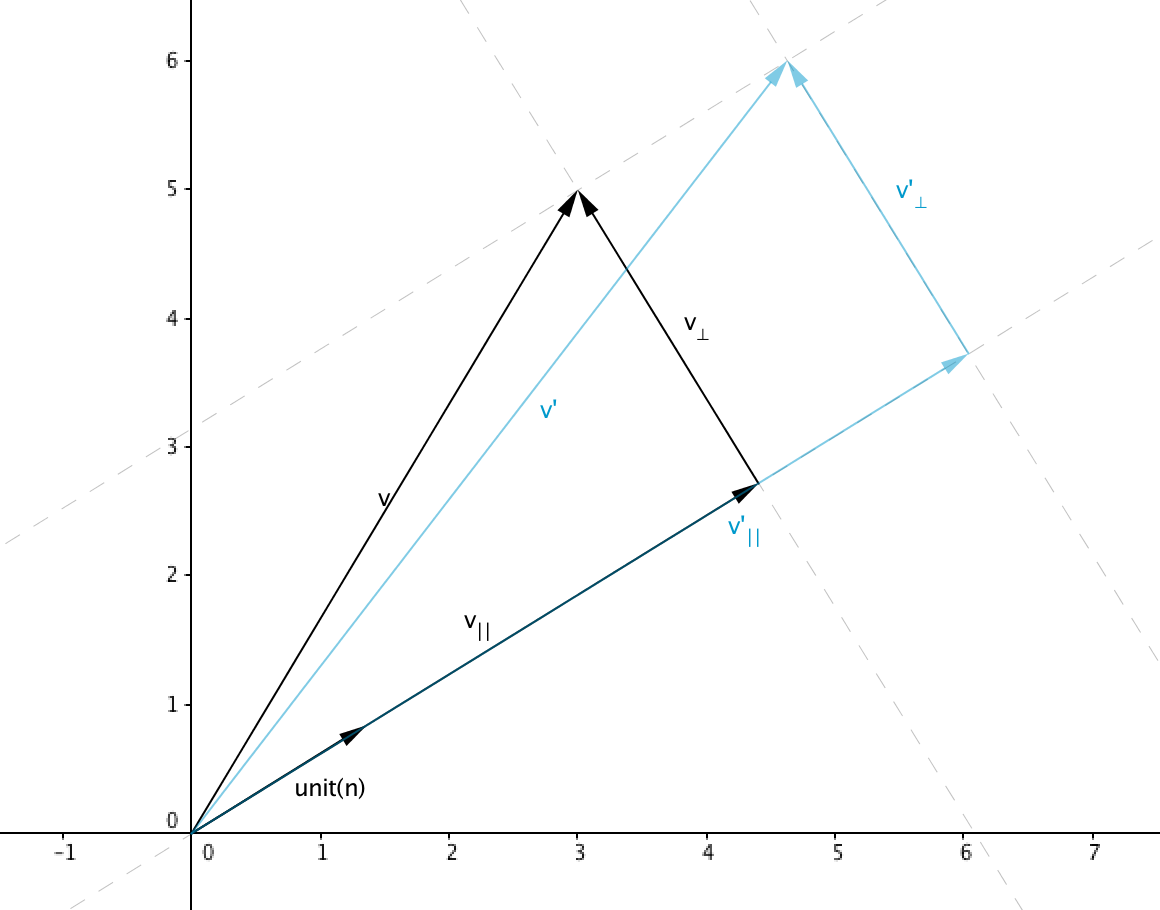
scale arbitrary axis

Separate $\mathbf{v}$ in two vectors, a vector parallel to $\unit{v}$ called $\mathbf{v_{\parallel}}$ and a vector perpendicular to $\unit{v}$ called $\mathbf{v_{\perp}}$ such that

$$ \mathbf{v} = \mathbf{v_{\parallel}} + \mathbf{v_{\perp}} $$

Where

$$ \begin{align*} \mathbf{v_{\parallel}} &= (\mathbf{v} \cdot \unit{n}) \unit{n} \\ \mathbf{v_{\perp}} &= \mathbf{v} - \mathbf{v_{\parallel}} \end{align*} $$

We can also represent $\mathbf{v’}$ as a sum of two vectors parallel and perpendicular to $\unit{n}$

$$ \mathbf{v'} = \mathbf{v_{\parallel}'} + \mathbf{v_{\perp}'} $$

Note that any vector that lies in the 2d line or 3d plane perpendicular to $\unit{n}$ will not be affected by the scale operation so $\mathbf{v’} = \mathbf{v_{\parallel}’} + \mathbf{v_{\perp}}$

Since $\mathbf{v_{\parallel}}$ is parallel to the direction of scale then $\mathbf{v_{\parallel}’} = k\mathbf{v_{\parallel}}$

Reconstructing the solution from the observations above

$$ \begin{align*} \mathbf{v_{\parallel}} &= (\mathbf{v} \cdot \unit{n}) \unit{n} \\ \mathbf{v_{\perp}'} &= \mathbf{v_{\perp}} \\ &= \mathbf{v} - \mathbf{v_{\parallel}} \\ &= \mathbf{v} - (\mathbf{v} \cdot \unit{n}) \unit{n} \\ \mathbf{v_{\parallel}'} &= k\mathbf{v_{\parallel}} \\ &= k(\mathbf{v} \cdot \unit{n}) \unit{n} \\ \mathbf{v'} &= \mathbf{v_{\perp}'} + \mathbf{v_{\parallel}'} \\ &= \mathbf{v} - (\mathbf{v} \cdot \unit{n}) \unit{n} + k(\mathbf{v} \cdot \unit{n}) \unit{n} \\ &= \mathbf{v} + (k - 1) (\mathbf{v} \cdot \unit{n}) \unit{n} \end{align*} $$

We can construct a general scale matrix by computing the vectors resulting after transforming the basis vectors $\mathbf{p}$, $\mathbf{q}$ and $\mathbf{r}$, for example let’s transform $\mathbf{p} = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}^T$

$$ \begin{align*} \mathbf{p'} &= \mathbf{p} + (k - 1) (\mathbf{p} \cdot \unit{n}) \unit{n} \\ &= \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + (k - 1) \left ( \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \begin{bmatrix} n_x \\ n_y \\ n_z \end{bmatrix}^T \right ) \begin{bmatrix} n_x \\ n_y \\ n_z \end{bmatrix} \\ &= \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + (k - 1) n_x \begin{bmatrix} n_x \\ n_y \\ n_z \end{bmatrix} \\ &= \begin{bmatrix} 1 + (k - 1) {n_x}^2 \\ (k - 1)n_xn_y \\ (k - 1)n_xn_z \end{bmatrix} \end{align*} $$

Similarly the values of $\mathbf{q’}$ and $\mathbf{r’}$ can be found which make the general rotation matrix equal to

$$ \begin{align*} \mathbf{S}(\unit{n}, k) &= \begin{bmatrix} \mathbf{p'} & \mathbf{q'} & \mathbf{r'} \end{bmatrix} \nonumber \\ & = \begin{bmatrix} 1 + (k - 1) {n_x}^2 & (k - 1)n_yn_x & (k - 1)n_zn_x \\ (k - 1)n_xn_y & 1 + (k - 1) {n_y}^2 & (k - 1)n_zn_y \\ (k - 1)n_xn_z & (k - 1)n_yn_z & 1 + (k - 1) {n_z}^2 \end{bmatrix} \end{align*} $$