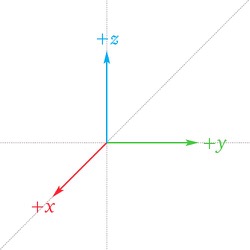
Euler angles are three angles used to describe the orientation of a rigid body, they are typically denoted
Intrinsic and extrinsic rotations
Intrinsic rotations
A set of intrinsic rotations represent rotations relative to the object space which changes after each rotation
If the axes of some coordinate system are
- perform a rotation of
- perform a rotation of
- perform a rotation of

A rotation matrix (used to pre-multiply column vectors) can be used to represent a sequence of intrinsic rotations, for example the extrinsic rotations
Where
Extrinsic rotations
A set of extrinsic rotations represent rotations relative to a fixed coordinate system (typically the world coordinate system), for example the set of extrinsic rotations
- perform a rotation of
- perform a rotation of
- perform a rotation of
A rotation matrix (used to pre-multiply column vectors) can be used to represent a sequence of intrinsic rotations, for example the extrinsic rotations
Where
Conversion between intrinsic rotations and extrinsic rotations
Any intrinsic rotation is equivalent to an extrinsic rotation by the same angles but with inverted order of rotations
For example the intrinsic rotations
Proper Euler angles
A sequence of three elemental rotations are called proper Euler angles when the first and third rotation axes are the same

Proper Euler angles representing rotations about
There are six possibilities of choosing the rotation axes for proper Euler angles which are intrinsic rotations in a similar way there are other six other possibilities of choosing the rotation axes which are extrinsic rotations
| intrinsic rotations | extrinsic rotations |
|---|---|
Tait-Bryan angles
A sequence of three elemental rotations are called Tail-Bryan angles when the angles represent rotations about three distinct axes
Just like proper Euler angles there are 6 possible intrinsic rotations and 6 possible extrinsic rotations
| intrinsic rotations | extrinsic rotations |
|---|---|
The set of intrinsic rotations

The rotation matrix for the sequence
Extrinsic rotations expressed in upright space
An important thing to note is that the standard rotation matrices work in upright space, if the object space axes are not aligned with the upright space axes (different direction) then the sequence of extrinsic rotations must be done on the axes expressed in upright space
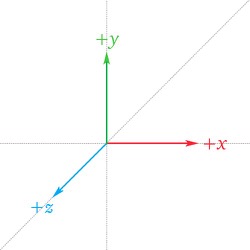
For example given that world space is
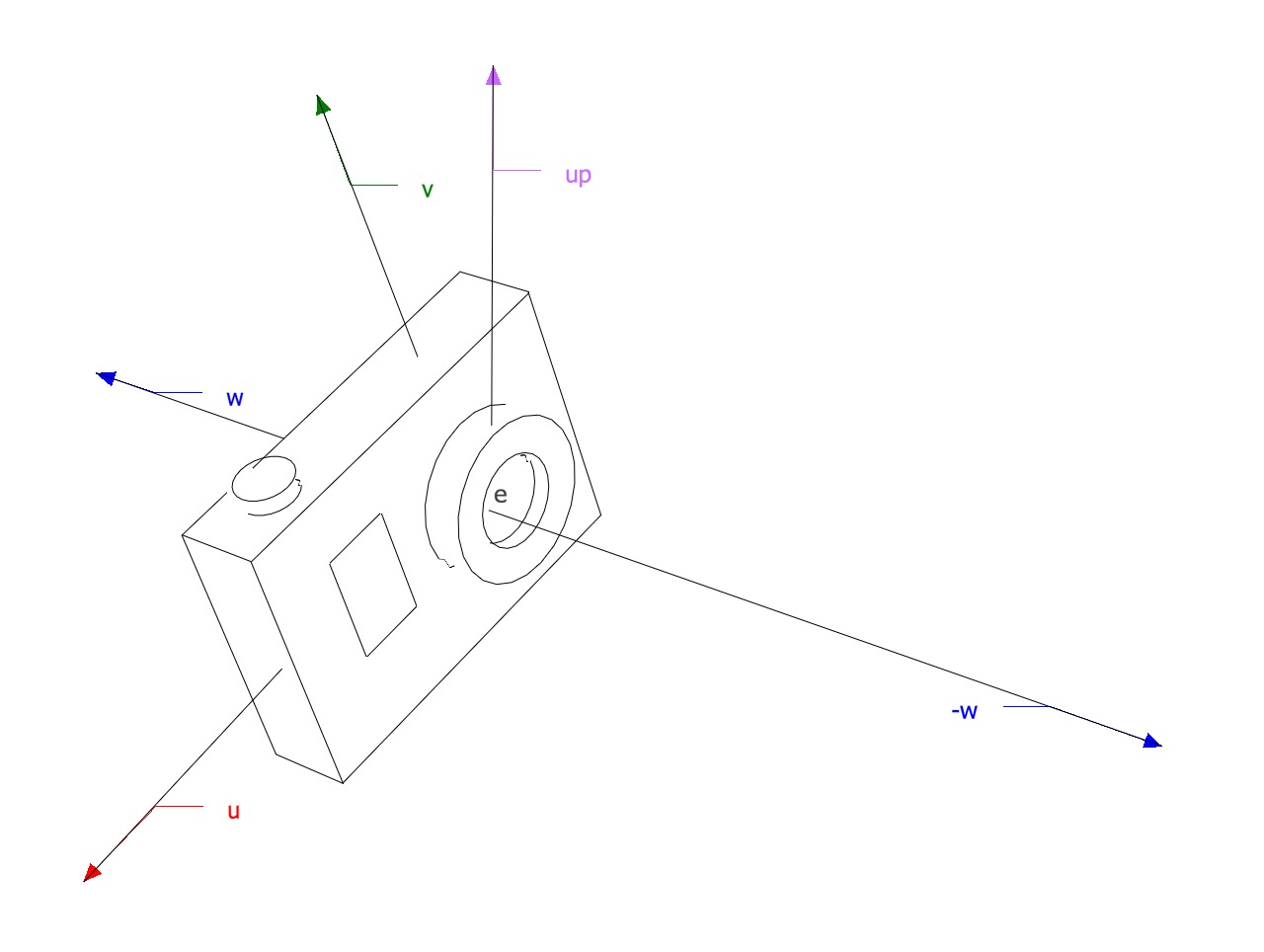
If there’s an object whose object space axes
Where
The problem can be simplified when frame is somewhat aligned with the upright space (the order might be different and the axis directions might be reversed but it’s still aligned), the following diagram shows some of these simplifications
| To/from | Description | Intrinsic/Extrinsic rotations |
Equivalence in world space |
|---|---|---|---|
 |
yaw, pitch, roll |
|
|
 |
yaw, pitch, roll |
|
|
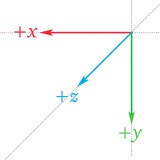 |
yaw, pitch, roll |
|
|