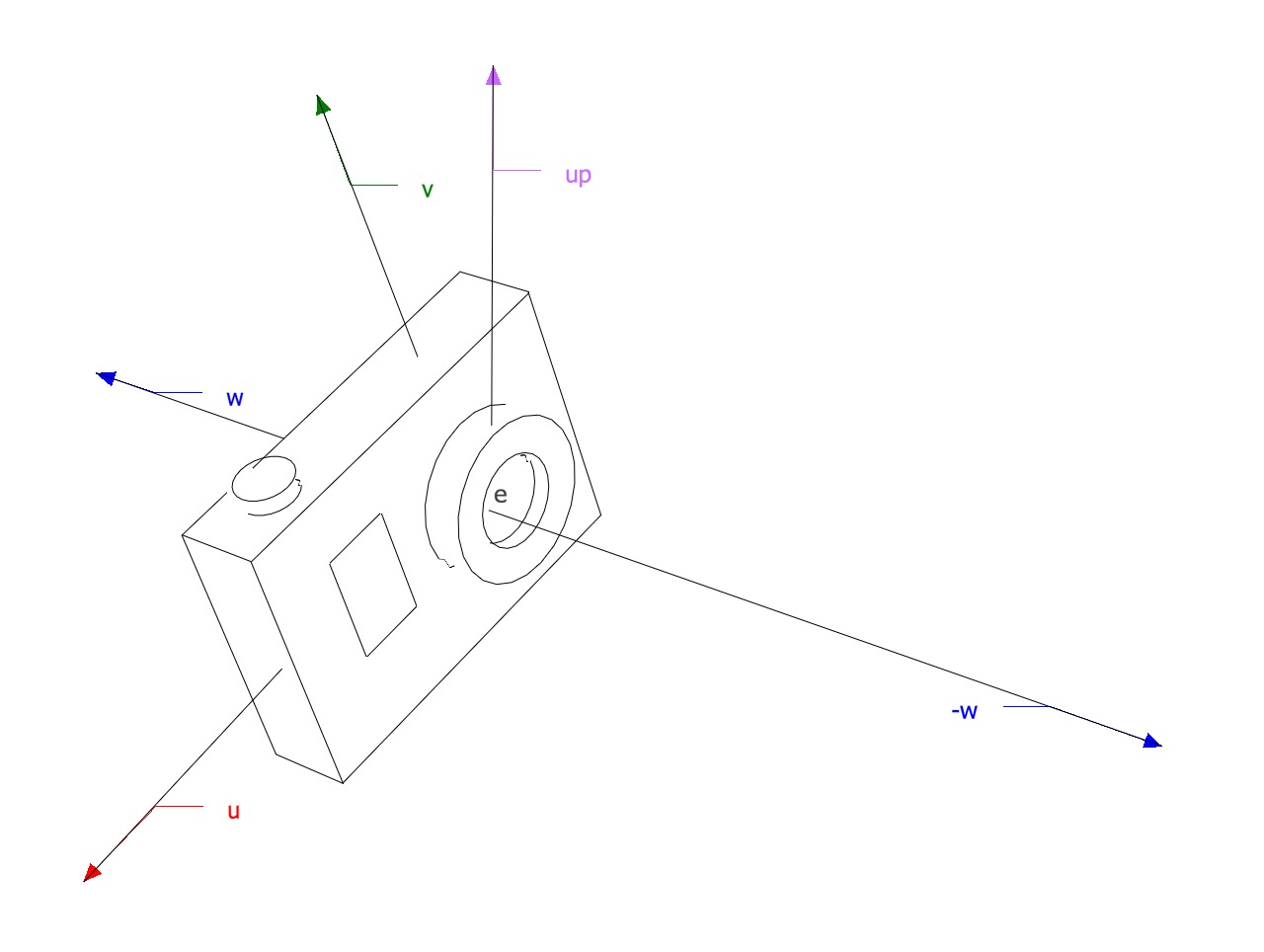
There’s a problem when the objects transformed to NDC need to be rasterized, some objects that are behind the eye might be rendered leading to incorrect results

For example when the perspective projection matrix is used all the points’ $z$-coordinate will be mapped to NDC using

If $n,f$ are the locations of the near and far plane in the negative $z$-axis in camera space and

Note that the equations above assume that $n,f \geq 0, n \leq f$ because $A$ and $B$ were already mapped using $-n \mapsto -1$ and $-f \mapsto 1$, for example when $n = 1$ and $f = 10$ the possible values can be described with the following plot

We see that objects behind the camera (points with $z_{cam} > 0$) are mapped to NDC as $z_{ndc} > 1$ i.e. in NDC points behind the camera are visible

For this reason there’s a preceding step in the rasterization process called clipping that removes parts of primitives that are outside the view volume (clipping against the six faces of the view volume), a basic implementation of the clipping process is described below

input: triangle, 6 planes of the view volume

for (each of the six planes) do
  if (the triangle is entirely outside the plane) then
    discard the triangle
  else if (the triangle passes through the plane) then
    clip the triangle
    if (the triangle is now a quadrilateral) then
      break the quadrilateral into two triangles

Culling is a process where geometry that’s not visible from the camera is discarded to save processing time

• View volume culling - Geometry outside the view volume can be culled since it won’t produce fragments when rasterized, this process is specially useful when triangles are grouped into an object that has an associated bounding volume, then
• Backface culling - polygons that face away from the camera can be culled before the pipeline starts

References