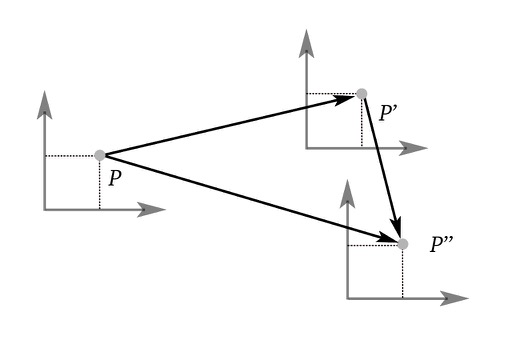
Line-line intersection

Given two lines in 3D, defined as rays:

$$ r_1(t_1) = \mathbf{p_1} + t_1 \mathbf{d_1} \\ r_2(t_2) = \mathbf{p_2} + t_2 \mathbf{d_2} $$

Where $t_1, t_2 \in \mathbb{R}$, the two lines intersect if:

$$ \mathbf{p_1} + t_1 \mathbf{d_1} = \mathbf{p_2} + t_2 \mathbf{d_2} $$

We can apply the cross multiplication operation on both sides with $\mathbf{d_2}$ and work from there to find the value of $t_1$.

$$ t_1 = \frac{\norm{(\mathbf{p_2} - \mathbf{p_1}) \times \mathbf{d_2} }}{ \norm{\mathbf{d_1} \times \mathbf{d_2}}} $$

Similarly, we can find the value of $t_2$ by crossing with $\mathbf{d_1}$ and work from there to find the value of $t_2$.

$$ t_2 = \frac{\norm{ (\mathbf{p_2} - \mathbf{p_1}) \times \mathbf{d_1}} }{ \norm{\mathbf{d_1} \times \mathbf{d_2}}} $$

The proof can be found here .

We can actually solve this problem graphically by using triangle similarity . Imagine the following situation:

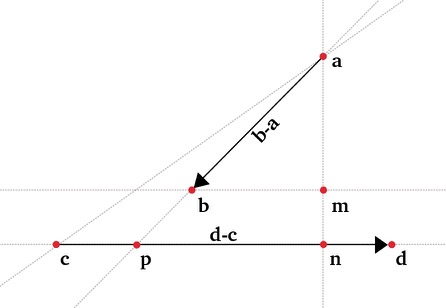
line line intersection

line line intersection

The intersection point $\mathbf{p}$ is equal to:

$$ \begin{equation} \label{line-line-intersection-point} \begin{split} \mathbf{p} &= \mathbf{a} + \norm{\mathbf{p - a}} \unit{ \mathbf{b - a} } \\ &= \mathbf{a} + \norm{\mathbf{p - a}} \frac{ \mathbf{b - a} }{ \norm{\mathbf{b - a}} } \end{split} \end{equation} $$

By triangle similarity, we see that:

$$ \frac{ \norm{\mathbf{p - a}} }{ \norm{\mathbf{b - a}} } = \frac{ \norm{\mathbf{n -a}} }{ \norm{\mathbf{m - a}} } $$

Multiplying the left side with an identity

$$ \begin{equation} \label{line-line-triangle-similarity} \frac{ \norm{\mathbf{p - a}} }{ \norm{\mathbf{b - a}} } = \frac{ \norm{\mathbf{n -a}} }{ \norm{\mathbf{m - a}} } \frac{ \norm{\mathbf{d - c}} }{ \norm{\mathbf{d - c}} } \end{equation} $$

We see that the quantity $\norm{ \mathbf{ n - a } } \norm{\mathbf{d - c}}$ is equal to the area of a parallelogram. We can skew the parallelogram (in the graphic, towards the $x$-axis) so that the left side becomes $\mathbf{c - a}$ and the bottom side $\mathbf{d - c}$ (which is not affected by the skew). Note that the area can also be expressed with the cross product of the vectors $\mathbf{c - a}$ and $\mathbf{d - c}$. Therefore,

$$ \begin{equation} \label{numerator-area} \norm{\mathbf{n - a}} \norm{\mathbf{d - c}} = \norm{(\mathbf{c - a}) \times (\mathbf{d - c})} \end{equation} $$

A similar equation can be derived for the parallelogram with sides $\mathbf{m - a}$ and $\mathbf{d - c}$, only this time the skewed side will become $\mathbf{b - a}$

$$ \begin{equation} \label{denominator-area} \norm{\mathbf{m - a}} \norm{\mathbf{d - c}} = \norm{(\mathbf{b - a}) \times (\mathbf{d - c})} \end{equation} $$

Replacing \eqref{numerator-area} and \eqref{denominator-area} in \eqref{line-line-triangle-similarity} and \eqref{line-line-intersection-point}, we see that the intersection point is equal to:

$$ \mathbf{p} = \mathbf{a} + (\mathbf{b - a}) \frac{ \norm{(\mathbf{c - a}) \times (\mathbf{d - c})} }{ \norm{(\mathbf{b - a}) \times (\mathbf{d - c})} } $$