The objective of this step is to find a transformation matrix to transform points expressed in world space to view space, a camera can be imagined to exist from a known point of view that captures some objects of the space
The construction of the transformation matrix to transform points from world space to view space needs 3 parameters:
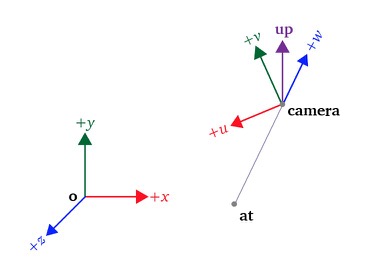
- $\mathbf{camera}$ a point expressed in world space defining the location of the point of view, note that the $\mathbf{camera}$ is at the origin of the view space
- $\mathbf{at}$ the direction where the camera is aiming at
- $\mathbf{up}$ denotes the upward orientation of the camera (typically coincides with the positive $y$-axis)

view transform
Note that the camera is looking at the negative $z$-axis of the view space, this is a convention rather than a rule since the projection matrix will be constructed in a way so that points in the $-z$-axis in view space are transformed to the range $[-1,1]$
Derivation of the view transform matrix
The process of transforming the vertices in the world space to view space is given by
- Creation of a coordinate frame for the view space
- Application of the appropriate translation for the camera location (world space -> upright space)
- Transformation of the points in world space to camera space (upright space -> object space)
Creation of a coordinate frame for the view space
Given $\mathbf{camera}$, $\mathbf{at}$ and $\mathbf{up}$ the steps to compute the coordinate frame are whose basis vectors are $\mathbf{u}$, $\mathbf{v}$ and $\mathbf{w}$ (note that since these are basis vectors they need to be unit vectors)
- compute $\mathbf{w}$ trivially by normalizing the vector $\mathbf{camera - at}$
- next $\mathbf{u}$ can be computed with the cross product of $\mathbf{w}$ and $\mathbf{up}$, again the resulting vector must be normalized
- finally $\mathbf{v}$ can be computed as
Camera translation
The transformation matrix that moves all the points from world space to view’s upright space is
Transformation of the points from world space to view space
Given that the camera transformation basis vectors (encoded in a matrix) are
Expressed in a 4x4 matrix
Works as a transformation matrix to transform points from view space to world space, therefore the matrix that does the opposite operation (transformation from world space to view space) is the inverse of this matrix (the transpose is equivalent since the matrix is orthonormal)
The view matrix
We can combine the translation and the rotation matrix in a single matrix called the view matrix which has the form