There's a total of 2 articles.
Cut-vertices (articulation points) in Graph Theory → Read more...
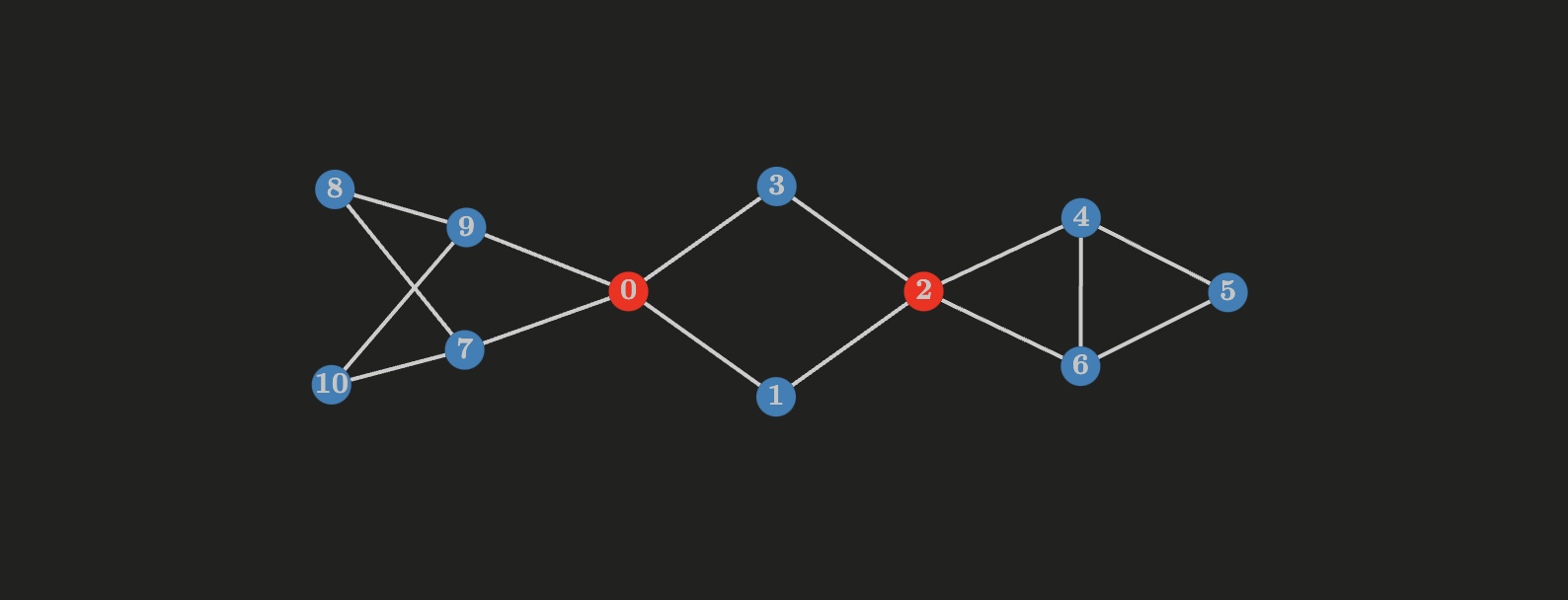
A vertex $v$ in a connected graph $G$ is called a cut-vertex if $G - v$ results in a disconnected graph, note that $G - v$ is an induced subgraph of $G$ (meaning that $G - v$ contains all the vertices of $G$ but $v$ and a set of edges $G - V$ where $V$ consists of all the edges incident to $v$).
In this article I implement an algorthm to find the articulation points in an undirected graph, also I explain biconnected components in an undirected graph and explain concepts such as edge connectivity and vertex connectivity.
Cut-edges (bridges) in Graph Theory → Read more...
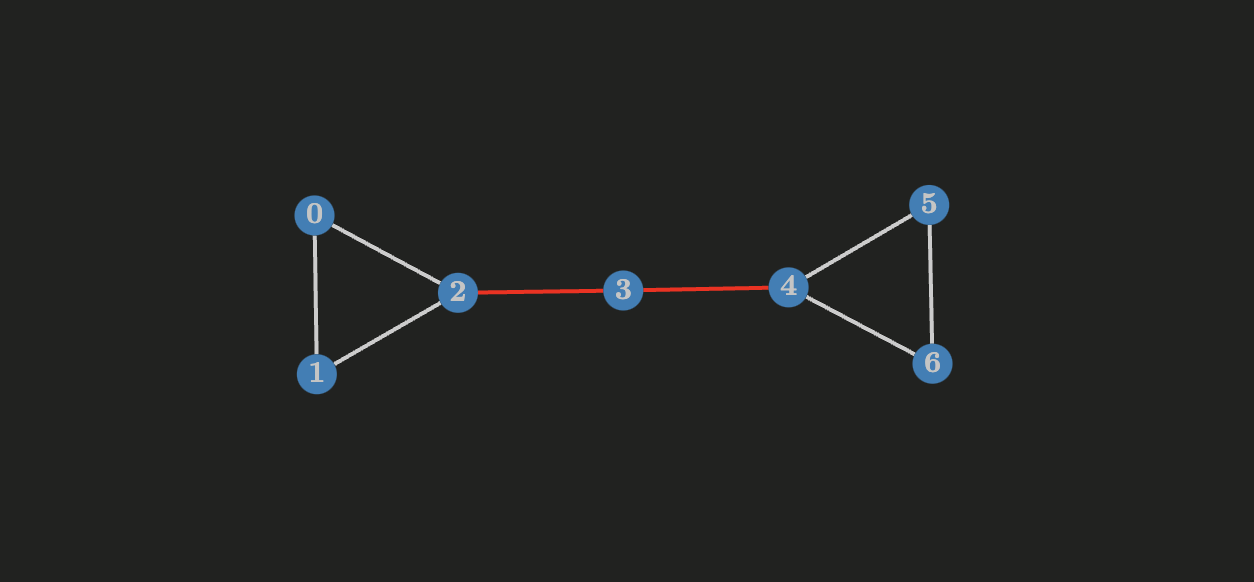
An edge $e = uv$ of a connected graph $G$ is called a bridge if $G - e$ is disconnected (it increases the number of components).
In this article I implement an algorthm to find the bridges of an undirected graph using DFS. Next I describe an algorithm to find strong bridges in directed graphs.