Introduction

A Bayesian network is a directed graph in which each node is annotated with quantitative probability information. The full specification is as follows:

  1. Each node corresponds to a random variable, which may be discrete or continuous.
  2. A set of directed links or arrows connects pairs of nodes. If there is an arrow from node $X$ to node $Y$, $X$ is said to be a parent of $Y$. The graph has no directed cycles (and hence is a directed acyclic graph, or DAG.
  3. Each node $X_i$ has a conditional probability distribution $P(X_i|Parents(X_i))$ that quantifies the effect of the parents on the node.
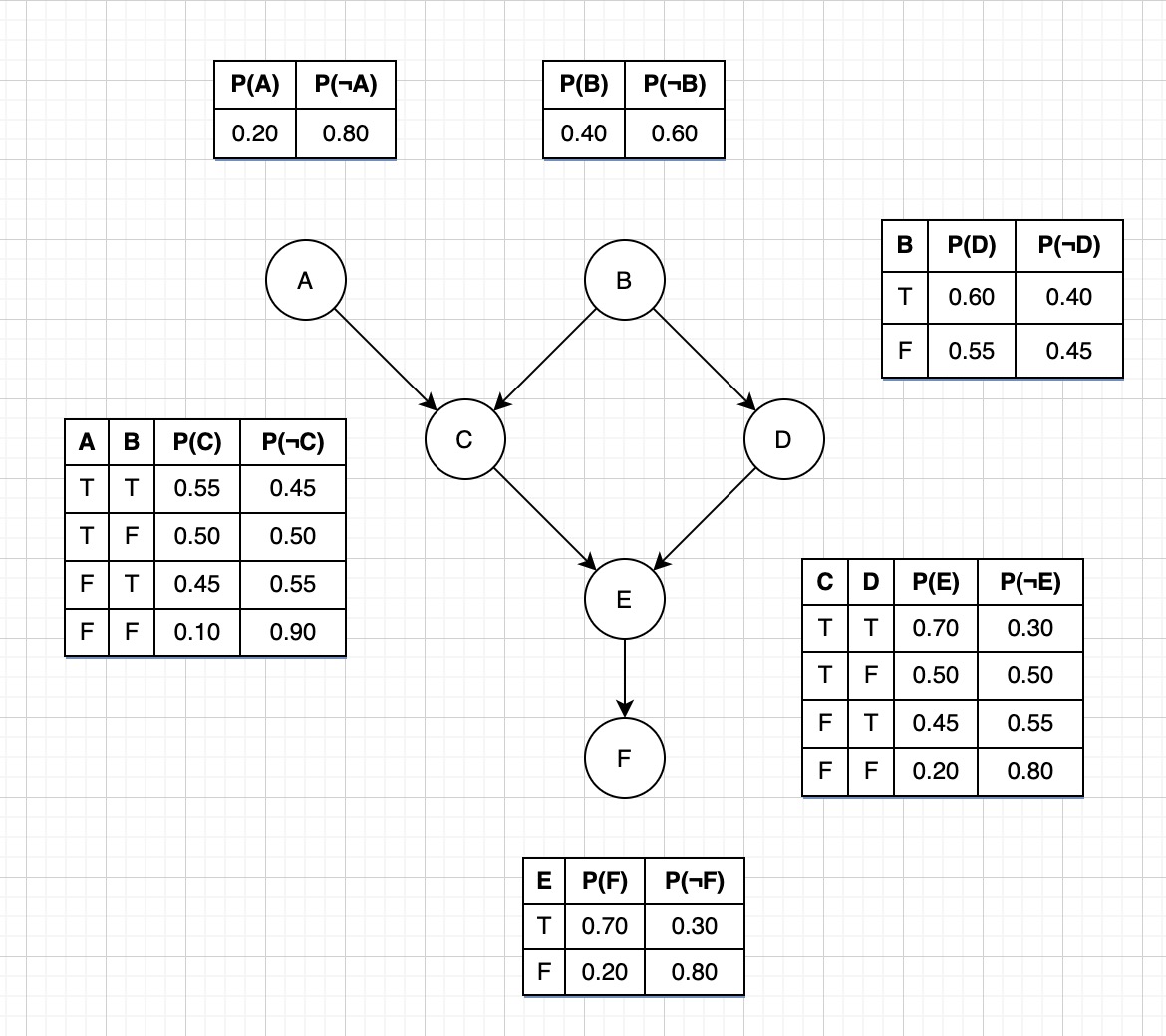
Example Bayesian Network

Example Bayesian Network

Semantics of a bayesian network:

  • The network is a representation of a joint probability distribution
  • Encoding of a collection of conditional independence statements

Full joint distribution

Given by:

$$ \begin{align} P(x_1, \ldots, x_n) = \prod_{i=1}^{N} P(x_i|Parents(X_i)) \end{align} $$

Which can be rewritten as:

$$ \begin{align*} P(x_1, \ldots, x_n) &= P(x_n | x_{n-1}, \ldots x_1) P(x_{n-1}, \ldots, x_1) \\ &= P(x_n | x_{n-1}, \ldots x_1) P(x_{n-1} | x_{n-2}, \ldots, x_1) \cdots P(x_2 | x_1) P(x_1) \\ &= \prod_{i=1}^{N} P(x_i | x_{i-1}, \ldots x_1) \;\; \text{(identity known as chain rule)} \end{align*} $$

The above is equivalent to

$$ P(X_i | X_{i-1}, \ldots X_1) = P(X_i|Parents(X_i)) $$

Provided that $Parents(X_i) \subseteq { X_{i-1}, \ldots, X_1 }$

Conditional independence relations in bayesian networks

Steps to determine if two variables are conditionally independent

  1. Draw the ancestral graph Construct the “ancestral graph” of all variables mentioned in the probability expression. This is a reduced version of the original net, consisting only of the variables mentioned and all of their ancestors (parents, parents’ parents, etc.)
  2. Moralize the ancestral graph by marrying the parents For each pair of variables with a common child, draw an undirected edge (line) between them. (If a variable has more than two parents, draw lines between every pair of parents.)
  3. Disorient the graph by replacing the directed edges (arrows) with undirected edges (lines).
  4. Delete the givens and their edges. If the independence question had any given variables, erase those variables from the graph and erase all of their connections, too.
  5. Given a query between two variables A, B
  6. If the variables are disconnected then they’re independent
  7. If the variables are connected then they’re dependent
  8. If the variables are missing because they were a given, they’re independent

In the following example we skip step 1 and moralize the entire bayesian network

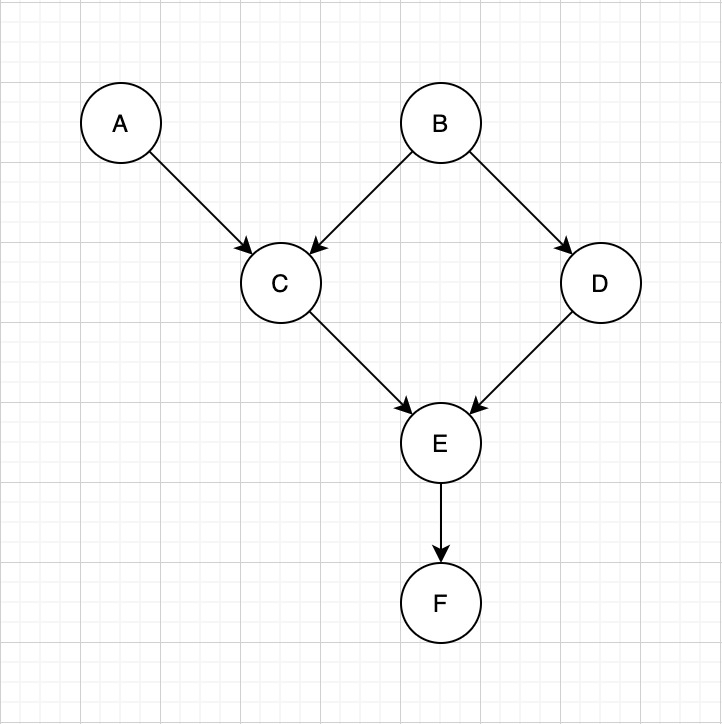
Example Bayesian Network

Example Bayesian Network

Example Bayesian Network Moralized

Example Bayesian Network Moralized

Some conditional independence queries ($\ci$ meaning conditionally independent of), delete the givens and their edges to check the connection between the query variables:

  • Is $A \ci B \given C$? No, there is a path A-B
  • Is $A \ci E \given C$? No, there is a path A-B-D-E
  • Is $A \ci E \given C,D$? Yes, there isn’t a path between A and E
  • Is $A \ci D \given C$? No, there is a path A-B-D
  • Is $B \ci E \given C$? No, there is a path B-D-E
  • Is $A \ci F \given C$? No, there is a path A-B-D-E-F
  • Is $A \ci F \given C,D$? Yes, there isn’t a path between A and F

Exact inference

Compute the posterior probability distribution for a set of query values given some observed event (set of evidence variables)

By enumeration

Any conditional probability can be computed by summing terms from the full joint distribution

$$ \textbf{P}(X \given \textbf{e}) = \alpha \textbf{P} (X, \textbf{e}) = \alpha \sum_{y} \textbf{P} (X, \textbf{e}, \textbf{y}) $$

Working with the example below we can answer some queries:

Example Bayesian Network

Example Bayesian Network

$$ \newcommand\g[1]{\color{gray}{#1}} $$
$$ \begin{align*} P(c|a) &= \alpha \sum_{b} P(a) P(b) P(c \given a,b) \\ &= \alpha P(a) \sum_{b} P(b) P(c \given a,b) \\ &= \alpha P(a) \sum_{b} \bordermatrix{\g{b} & \g{\neg b}}{}{\begin{bmatrix} 0.4 & 0.6 \end{bmatrix}} \bordermatrix{\g{b} & \g{\neg b}}{\g{c} \\ \g{\neg c}}{\begin{bmatrix} 0.55 & 0.5 \\ 0.45 & 0.5 \end{bmatrix}} \\ &= \alpha P(a) \sum_{b} \bordermatrix{\g{b} & \g{\neg b}}{\g{c} \\ \g{\neg c}}{\begin{bmatrix} 0.22 & 0.3 \\ 0.18 & 0.3 \end{bmatrix}} \\ &= \alpha \; 0.2 \; \bordermatrix{}{\g{c} \\ \g{\neg c}}{\begin{bmatrix} 0.52 \\ 0.48 \end{bmatrix}} \\ &= \bordermatrix{}{\g{c} \\ \g{\neg c}}{\begin{bmatrix} 0.104 \\ 0.096 \end{bmatrix}} \\ &= \alpha [.104, .096] \\ &= [\textbf{0.52}, 0.48] \end{align*} $$
$$ \begin{align*} P(e|\neg c, b) &= \alpha \sum_{a,d,f} P(a) P(b) P(\neg c \given a,b) P(d \given b) P(e \given \neg c,d) P(f \given e) \\ &= \alpha P(b) \sum_{a} P(a) P(\neg c \given a,b) \sum_{d} P(d \given b) P(e \given \neg c,d) \sum_{f} P(f \given e) \\ &= \alpha P(b) \sum_{a} P(a) P(\neg c \given a,b) \sum_{d} P(d \given b) P(e \given \neg c,d) \sum_{f} \bordermatrix{\g{f} & \g{\neg f}}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 0.7 & 0.3 \\ 0.2 & 0.8 \end{bmatrix}} \\ &= \alpha P(b) \sum_{a} P(a) P(\neg c \given a,b) \sum_{d} P(d \given b) P(e \given \neg c,d) \bordermatrix{}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 1 \\ 1 \end{bmatrix}} \\ &= \alpha P(b) \sum_{a} P(a) P(\neg c \given a,b) \sum_{d} \bordermatrix{\g{d} & \g{\neg d}}{}{\begin{bmatrix} 0.6 & 0.4 \end{bmatrix}} \bordermatrix{\g{d} & \g{\neg d}}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 0.45 & 0.2 \\ 0.55 & 0.8 \end{bmatrix}} \bordermatrix{}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 1 \\ 1 \end{bmatrix}} \\ &= \alpha P(b) \sum_{a} P(a) P(\neg c \given a,b) \sum_{d} \bordermatrix{\g{d} & \g{\neg d}}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 0.27 & 0.08 \\ 0.33 & 0.32 \end{bmatrix}} \\ &= \alpha P(b) \sum_{a} P(a) P(\neg c \given a,b) \bordermatrix{}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 0.35 \\ 0.65 \end{bmatrix}} \\ &= \alpha P(b) \sum_{a} \bordermatrix{}{\g{a} \\ \g{\neg a}}{\begin{bmatrix} 0.2 \\ 0.8 \end{bmatrix}} \bordermatrix{\g{\neg c, b}}{\g{a} \\ \g{\neg a}}{\begin{bmatrix} 0.45 \\ 0.55 \end{bmatrix}} \bordermatrix{}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 0.35 \\ 0.65 \end{bmatrix}} \\ &= \alpha P(b) \sum_{a} \bordermatrix{}{\g{a} \\ \g{\neg a}}{\begin{bmatrix} 0.09 \\ 0.44 \end{bmatrix}} \bordermatrix{}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 0.35 \\ 0.65 \end{bmatrix}} \quad \text{the element wise product is with unrelated bases so we do with $a^T$} \\ &= \alpha P(b) \sum_{a} \bordermatrix{\g{a} & \g{\neg a}}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 0.0315 & 0.154 \\ 0.0585 & 0.2275 \end{bmatrix}} \\ &= \bordermatrix{}{\g{e} \\ \g{\neg e}}{\begin{bmatrix} 0.1855 \\ 0.286 \end{bmatrix}} \quad \text{$P(b)$ is not a factor, it's an evidence} \\ &= \alpha [0.1855, 0.286] \\ &= [\textbf{0.393425239}, 0.606574761] \end{align*} $$

Reading