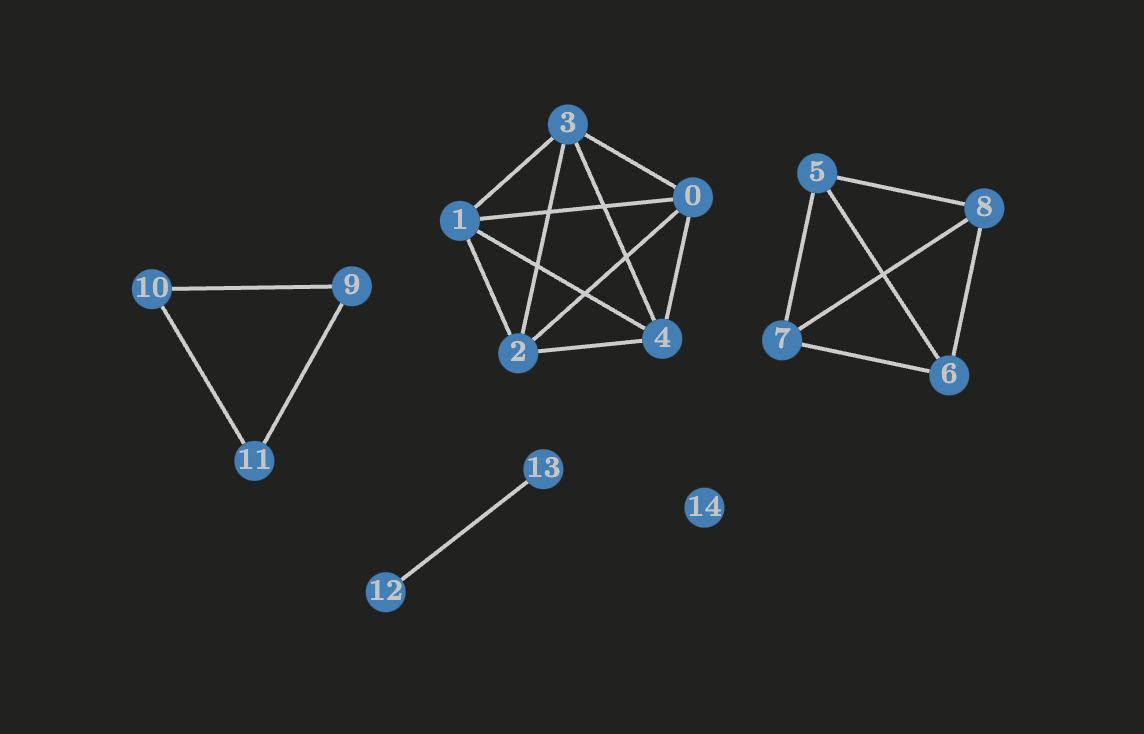
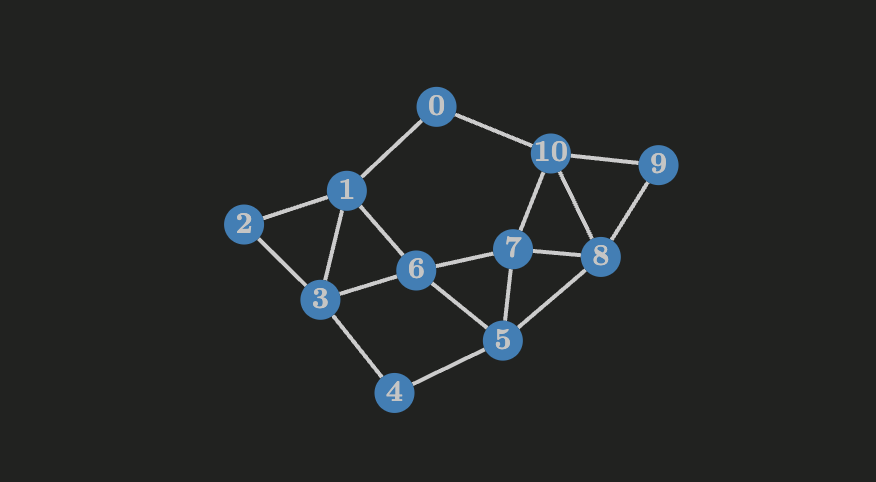
Breadth First Search (BFS)

Given a graph $G$ and a distinguished source vertex $s$, BFS explores the edges of $G$ to discover the vertices adjacent to $s$, as a consequence it also computes the distance of the path from $s$ to each reachable vertex

vector<int> dist;
vector<int> parent;

/**
 * Traverses a graph `G` of order `n` and size `m` by breadth
 *
 * Time complexity: O(n + m)
 * Space complexity: O(n)
 *
 * @param {vector<vector<int> >} g The adjacency list representation
 * of a graph
 * @param {int} source The source vertex
 */
void bfs(vector<vector<int> > &g, int source) {
  int n = g.size();
  dist.assign(n, -1);
  parent.assign(n, -1);

  queue<int> remaining;
  dist[source] = 0;
  remaining.push(source);

  while (!remaining.empty()) {
    int current = remaining.front();
    remaining.pop();

    for (int i = 0; i < g[current].size(); i += 1) {
      int next = g[current][i];
      if (dist[next] == -1) {
        dist[next] = dist[current] + 1;
        parent[next] = current;
        remaining.push(next);
      }
    }
  }
}

Depth First Search (DFS)

Given a graph $G$ and a distinguished source vertex $s$, DFS explores the edges incident to $s$ and explores as far as possible along each branch before backtracking, to prevent infinite loops caused by visiting a vertex multiple times an additional state is used in each vertex which denotes if the vertex was visited before

Whenever a vertex $v$ is discovered by some vertex $u$, we say that $u$ is a predecesor of $v$, and also since every vertex can only have one predecessor (a vertex can only be visited once) during the traversal the algorithm forms a tree called the dfs tree

During the process of creation of the dfs tree the algorithm can also define timestamps on each vertex (an integer denoting the time an action happened)

• $v_{in}$ recorded when $v$ is first discovered
• $v_{out}$ recorded when the search finishes exploring $v$’s adjacent vertices

Properties

• the number of descendent of any vertex $v$ is equal to $\frac{v_f-v_d-1}{2}$
• for any two vertices $u$ and $v$ exactly one of the following holds
• if the interval $[u_{in},u_{out}]$ and $[v_{in},v_{out}]$ are disjoint intervals then neither $u$ is a descendant of $v$ nor $v$ a descendant of $u$ in the dfs tree
• if the interval $[u_{in},u_{out}]$ is contained in $[v_{in},v_{out}]$ then $u$ is a descendant of $v$
• if the interval $[v_{in},v_{out}]$ is contained in $[u_{in},u_{out}]$ then $v$ is a descendant of $u$

Classification of edges

We can define four edge types produced by a DFS on $G$

1. Tree edges, an edge $uv$ is a tree edge if $v$ was first discovered by $u$
2. Back edges, an edge $uv$ is a back edge if it connects $u$ with an antecesor of of $v$)
3. Forward edges, an edge $uv$ is a forward edge if it connects $u$ with a descendant of $v$ (nontree edge)
4. Cross edges, all the other edges, e.g. an edge between branches in the dfs tree

We can identify these edges with an additional state stored in the vertices of the graph during the dfs tree process, the additional state will be $v_{color}$ and can have three possible values

• $v_{color}=WHITE$ if a vertex wasn’t explored yet
• $v_{color}=GRAY$ when a vertex is discovered first
• $v_{color}=BLACK$ when a vertex has finished exploring its adjacent vertices

During the analysis of an edge we can take a look at the color of the adjacent vertex to determine the type of edge, given the edge $uv$ there are three possible outcomes

• if $v_{color}=WHITE$ then $uv$ is a tree edge
• if $v_{color}=GRAY$ then $uv$ is a back edge
• if $v_{color}=BLACK$ then $uv$ is a forward/cross edge

Another way to determine the type of edge is by analyzing the states $u_{in}$ ($u_{out}$ is undefined when all the edge $uv$ are being analyzed) and $v_{in},v_{out}$ of the incident vertices to the edge, given an edge $uv$

• if $v_{in}$ is not defined then $uv$ is a tree edge
• if $v_{in}$ is defined and $v_{out}$ is not defined then $uv$ is a back edge
• if $v_{in}$ is defined and $v_{out}$ is defined and $u_{in}<v_{in}$ then $uv$ is a forward edge
• if $v_{in}$ is defined and $v_{out}$ is defined and $u_{in}>v_{in}$ then $uv$ is a cross edge

Additional properties of the edges

• if $G$ is an undirected graph then every edge of $G$ is either a tree edge or a back edge during the exploration of the dfs tree
• a directed graph $G$ is acyclic if it contains no back edges

int time_spent = 0;

// the adjacency list of `G`
vector<vector<int> > g;
// the explored state of a vertex `i`
vector<bool> visited;
// the predecesor of a vertex `i` in the dfs tree
vector<bool> predecessor;
// the time a vertex `i` was discovered first
vector<int> time_in;
// the time a vertex `i` spent exploring each reachable non-visited vertices
vector<int> time_out;

/**
 * Traverses a graph `G` of order `n` and size `m` by depth,
 * it's assumed that `time_in`, `time_out`, `visited`, `predecessor`
 * are initialized correctly with a size equal to `n`
 *
 * Time complexity: O(n + m)
 * Space complexity: O(n)
 *
 * @param {int} v The current vertex being analyzed
 */
void dfs(int v) {
  visited[v] = true;
  time_in[v] = ++time_spent;

  for (int i = 0; i < g[v].size(); i += 1) {
    int next = g[v][i];

    // edge analysis
    if (!time_in[next]) {
      // edge (v, next) is a tree edge
    } else if (!time_out[next]) {
      // edge (v, next) is a back edge
    } else if (time_in[v] < time_in[next]) {
      // edge (v, next) is a forward edge
    } else {
      // edge (v, next) is a forward edge
    }

    // traversal to adjacent vertices
    if (!visited[next]) {
      predecessor[next] = v;
      dfs(next);
    }
  }

  time_out[v] = ++time_spent;
}