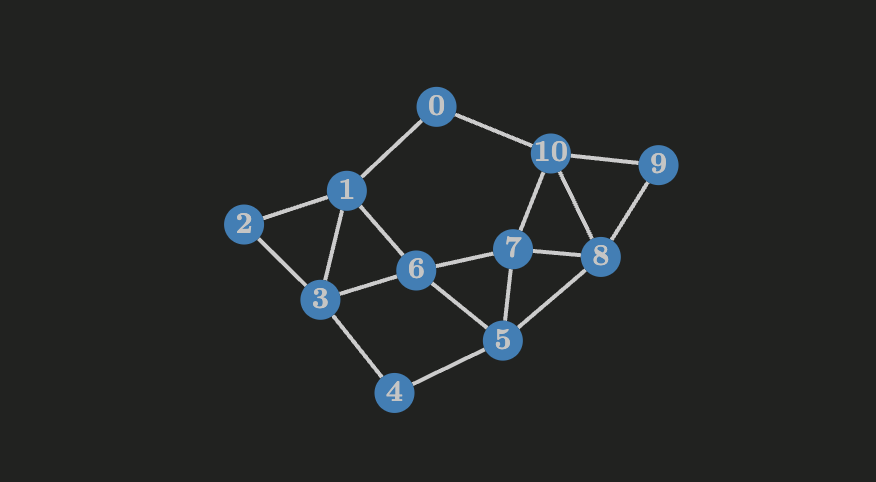
A connected subgraph of $G$ that is not a proper subgraph of any other connected subgraph of $G$ is a component of $G$; i.e., there’s a $u-v$ path in the mentioned subgraph.

Strongly connected components are useful in a variety of graph algorithms, including finding the shortest path between two vertices, detecting cycles in a graph, and determining the structure of a graph. They can be computed efficiently using algorithms such as Tarjan’s and Kosaraju’s algorithms.

Undirected graphs

The problem of finding components in an undirected graph requires a simple graph traversal starting from an arbitrary vertex, keeping track of the vertices that were already visited. It’s also necessary to run the algorithm above for every vertex of $G$ (given that it was not visited).

• The number of components of an undirected graph $G$ is equal to the number of disconnected subgraphs.

vector<bool> visited;
// adjacency list of G
vector<vector<int> > g;

void dfs(int v) {
  visited[v] = true;
  for (int i = 0; i < g[v].size(); i += 1) {
    int next = g[v][i];
    if (!visited[next]) {
      dfs(next);
    }
  }
}

/**
 * Computes the number of connected components in an undirected graph `G`
 * of order `n` and size `m`
 *
 * Time complexity: O(n + m)
 * Space complexity: O(n)
 *
 * @return {int} The number of components in `G`
 */
int connected_components() {
  int n = g.size();
  visited.assign(n, false);

  int components = 0;
  for (int i = 0; i < visited.size(); i += 1) {
    if (!visited[i]) {
      dfs(i);
      ++components;
    }
  }
  return components;
}

Directed graphs

Given a directed graph $G$, two nodes $u,v\in V(G)$ are called strongly connected if $v$ is reachable from $u$ and $u$ is reachable from $v$.

A strongly connected component (SCC) of $G$ is a subgraph $C\subseteq V(G)$ such that:

• $C$ is not empty.
• For any $u,v\in V(G)$, $u$ and $v$ are strongly connected.
• For any $u\in V(G)$ and $v\in G-C$, $u$ and $v$ are not strongly connected.

Tarjan’s algorithm

The idea is to perform a DFS from an arbitrary vertex (conducting subsequent DFS from non-explored vertices). During the traversal, each vertex $v$ is assigned two numbers:

• The time it was explored, denoted as $v_{time}$.
• The smallest index of any node known to be reachable from $v$, denoted as $v_{low}$.

Let $u$ be a node that belongs to an SCC. If $u$ is the arbitrary vertex chosen, then the only known vertex that is reachable from $u$ is $u$ itself. Let $v$ be a vertex discovered during the exploration of $u$. If there’s a $v\to u$ path, then it means that there’s a cycle, and all the vertices in the path $u-v$ belong to the same connected component. Such a node $u$ is called the root of the SCC.

Let $u$ be a node that belongs to an SCC. If it’s known that there’s a $u-v$ cycle and also that $u$ can reach a vertex $t$ with a lower index than $u$, then $v$ and $t$ belong to the same component.

A stack is also needed to keep track of the nodes that were visited. The working of the stack follows the invariant: a node remains on the stack after exploration if and only if it has a path to some node earlier in the stack.

// adjacency list of G
vector<vector<int> > g;

int time_spent;
// the number of scc
int total_scc;

// the time a vertex was discovered
vector<int> time_in;
// the smallest index of any vertex known to be reachable from `i`
vector<int> back;
// the scc vertex `i` belongs to
vector<int> scc;
// invariant: a node remains in the stack after exploration if
// it has a path to some node explored earlier that is in the stack
vector<bool> in_stack;
stack<int> vertices;

void dfs(int v) {
  int next;

  // the lowest back edge discovery time of `v` is
  // set to the discovery time of `v` initally
  back[v] = time_in[v] = ++time_spent;

  vertices.push(v);
  in_stack[v] = true;

  for (int i = 0; i < g[v].size(); i += 1) {
    next = g[v][i];
    if (time_in[next] == -1) {
      // unvisited edge
      dfs(next);
      // propagation of the lowest back edge discovery time
      back[v] = min(back[v], back[next]);
    } else if (in_stack[next]) {
      // (v, next) is a back edge only if it's connected to a predecessor
      // of `v`, i.e. if `next` is in same branch in the dfs tree
      //
      // an alternative is to use the time a vertex finished exploring its
      // adjacent nodes, if the time is not set then it's a back edge
      back[v] = min(back[v], time_in[next]);
    }
  }

  // if the root node of a connected component has finished
  // exploring all its neighbors, assign the same component `id`
  // to all the elements in the scc
  if (back[v] == time_in[v]) {
    total_scc += 1;
    do {
      next = vertices.top();
      vertices.pop();
      in_stack[next] = false;
      scc[next] = total_scc;
    } while (next != v);
  }
}

/**
 * Finds the strongly connected components in a digraph `G` of order `n`
 * and size `m`
 *
 * Time complexity: O(n + m)
 * Space complexity: O(n)
 *
 * @returns {int} the number of strongly connected components
 */
int tarjan() {
  int n = g.size();

  scc.assign(n, -1);
  time_in.assign(n, -1);
  back.assign(n, -1);
  in_stack.assign(n, false);
  while (!vertices.empty()) {
    vertices.pop();
  }

  time_spent = 0;
  total_scc = 0;

  for (int i = 0; i < n; i += 1) {
    if (time_in[i] == -1) {
      dfs(i);
    }
  }
  return total_scc;
}